Skip to content →

Tag: topology

changes (ahead)

Published January 19, 2011 by lievenlb

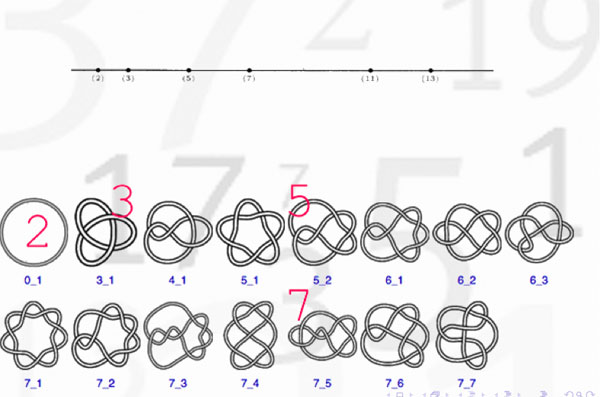
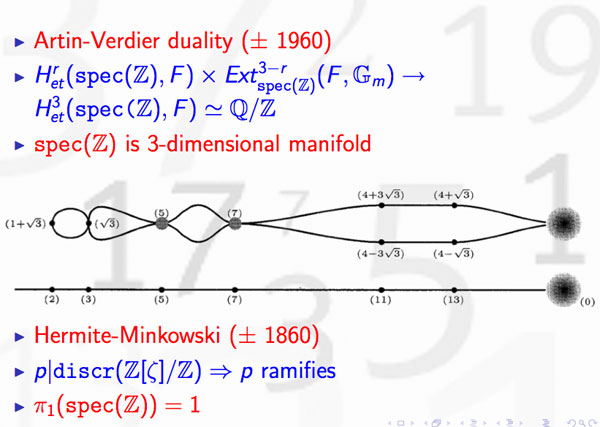
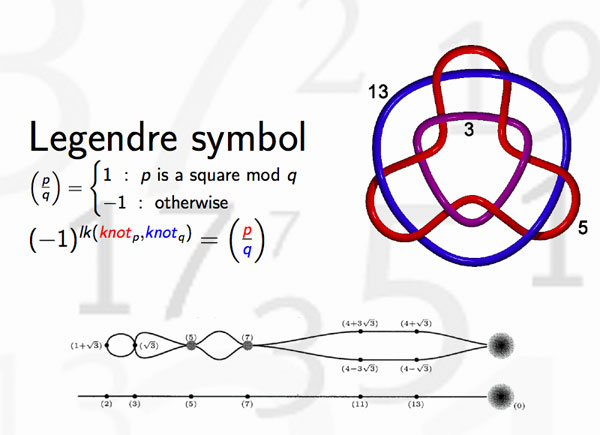
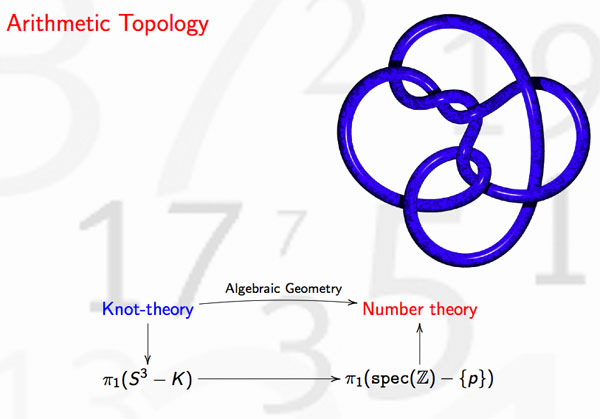
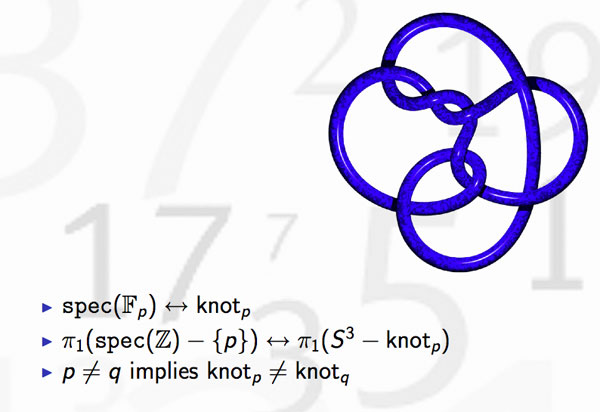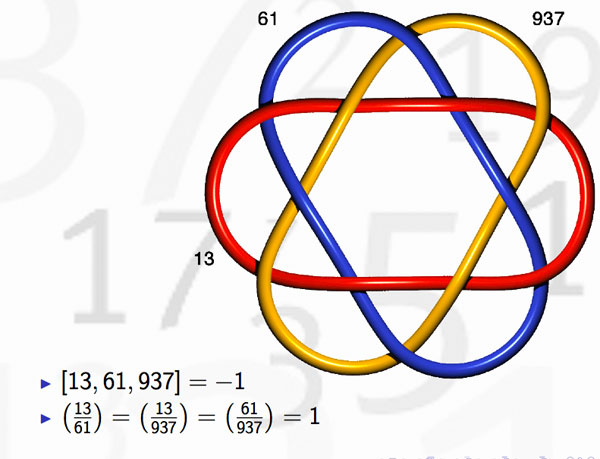In view or recents events & comments, some changes have been made or will be made shortly :

categories : Sanitized the plethora of wordpress-categories to which posts belong. At the moment there are just 5 categories : ‘stories’ and ‘web’ (for all posts with low math-content) and three categories ‘level1’, ‘level2’ and ‘level3’, loosely indicating the math-difficulty of a post.

MathJax : After years of using LatexRender and WP-Latex, we’ll change to MathJax from now on. I’ll try to convert older posts as soon as possible. (Update : did a global search and replace. ‘Most’ LaTeX works, major exceptions being matrices and xymatrix commands. I’ll try to fix those later with LatexRender.)

theme : The next couple of days, the layout of this site may change randomly as I’ll be trying out things with the Swift wordpress theme. Hopefully, this will converge to a new design by next week.

name : Neverendingbooks will be renamed to something more math-related. Clearly, the new name will depend on the topics to be covered. On the main index page a pop-up poll will appear in the lower right-hand corner after 10 seconds. Please fill in the topics you’d like us to cover (no name or email required).

This poll will close on friday 21st at 12 CET and its outcome will influence name/direction of this blog. Use it also if you have a killer newname-suggestion. Among the responses so far, a funnier one : “An intro to, or motivation for non-commutative geometry, aimed at undergraduates. As a rule, I’d take what you think would be just right for undergrads, and then trim it down a little more.”

guest-posts : If you’d like to be a guest-blogger here at irregular times, please contact me. The first guest-post will be on noncommutative topology and the interpretation of quantum physics, and will appear soon. So, stay tuned…

2 Comments

the Reddit (after)effect

Published January 15, 2011 by lievenlb

Sunday january 2nd around 18hr NeB-stats went crazy.

Referrals clarified that the post ‘What is the knot associated to a prime?’ was picked up at Reddit/math and remained nr.1 for about a day.

Now, the dust has settled, so let’s learn from the experience.

A Reddit-mention is to a blog what doping is to a sporter.

You get an immediate boost in the most competitive of all blog-stats, the number of unique vistors (blue graph), but is doesn’t result in a long-term effect, and, it may even be harmful to more essential blog-stats, such as the average time visitors spend on your site (yellow graph).

For NeB the unique vistors/day fluctuate normally around 300, but peaked to 1295 and 1733 on the ‘Reddit-days’. In contrast, the avg. time on site is normally around 3 minutes, but dropped the same days to 44 and 30 seconds!

Whereas some of the Reddits spend enough time to read the post and comment on it, the vast majority zap from one link to the next. Having monitored the Reddit/math page for two weeks, I’m convinced that post only made it because it was visually pretty good. The average Reddit/math-er is a viewer more than a reader…

So, should I go for shorter, snappier, more visual posts?

Let’s compare Reddits to those coming from the three sites giving NeB most referrals : Google search, MathOverflow and Wikipedia.

This is the traffic coming from Reddit/math, as always the blue graph are the unique visitors, the yellow graph their average time on site, blue-scales to the left, yellow-scales to the right.

Here’s the same graph for Google search. The unique visitors/day fluctuate around 50 and their average time on site about 2 minutes.

The math-related search terms most used were this month : ‘functor of point approach’, ‘profinite integers’ and ‘bost-connes sytem’.

More rewarding to me are referrals from MathOverflow.

The number of visitors depends on whether the MathO-questions made it to the front-page (for example, the 80 visits on december 15, came from the What are dessins d’enfants?-topic getting an extra comment that very day, and having two references to NeB-posts : The best rejected proposal ever and Klein’s dessins d’enfant and the buckyball), but even older MathO-topics give a few referrals a day, and these people sure take their time reading the posts (+ 5 minutes).

Other MathO-topics giving referrals this month were Most intricate and most beautiful structures in mathematics (linking to Looking for F-un), What should be learned in a first serious schemes course? (linking to Mumford’s treasure map (btw. one of the most visited NeB-posts ever)), How much of scheme theory can you visualize? (linking again to Mumford’s treasure map) and Approaches to Riemann hypothesis using methods outside number theory (linking to the Bost-Connes series).

Finally, there’s Wikipedia

giving 5 to 10 referrals a day, with a pretty good time-on-site average (around 4 minutes, peaking to 12 minutes). It is rewarding to see NeB-posts referred to in as diverse Wikipedia-topics as ‘Fifteen puzzle’, ‘Field with one element’, ‘Evariste Galois’, ‘ADE classification’, ‘Monster group’, ‘Arithmetic topology’, ‘Dessin d’enfant’, ‘Groupoid’, ‘Belyi’s theorem’, ‘Modular group’, ‘Cubic surface’, ‘Esquisse d’un programme’, ‘N-puzzle’, ‘Shabat polynomial’ and ‘Mathieu group’.

What lesson should be learned from all this data? Should I go for shorter, snappier and more visual posts, or should I focus on the small group of visitors taking their time reading through a longer post, and don’t care about the appallingly high bounce rate the others cause?

8 Comments

What is the knot associated to a prime?

Published January 2, 2011 by lievenlb

Sometimes a MathOverflow question gets deleted before I can post a reply…

Yesterday (New-Year) PD1&2 were visiting, so I merely bookmarked the What is the knot associated to a prime?-topic, promising myself to reply to it this morning, only to find out that the page no longer exists.

From what I recall, the OP interpreted one of my slides of the April 1st-Alumni talk

as indicating that there might be a procedure to assign to a prime number a specific knot. Here’s the little I know about this :

Artin-Verdier duality in etale cohomology suggests that $Spec(\mathbb{Z}) $ is a 3-dimensional manifold, as Barry Mazur pointed out in this paper

The theory of discriminants shows that there are no non-trivial global etale extensions of $Spec(\mathbb{Z}) $, whence its (algebraic) fundamental group should be trivial. By Poincare-Perelman this then implies that one should view $Spec(\mathbb{Z}) $ as the three-sphere $S^3 $. Note that there is no ambiguity in this direction. However, as there are other rings of integers in number fields having trivial fundamental group, the correspondence is not perfect.

Okay, but then primes should correspond to certain submanifolds of $S^3 $ and as the algebraic fundamental group of $Spec(\mathbb{F}_p) $ is the profinite completion of $\mathbb{Z} $, the first option that comes to mind are circles

Hence, primes might be viewed as circles embedded in $S^3 $, that is, as knots! But which knots? Well, as far as I know, nobody has a procedure to assign a knot to a prime number, let alone one having p crossings. What is known, however, is that different primes must correspond to different knots

because the algebraic fundamental groups of $Spec(\mathbb{Z})- { p } $ differ for distinct primes. This was the statement I wanted to illustrate in the first slide.

But, the story goes a lot further. Knots may be linked and one can detect this by calculating the link-number, which is symmetric in the two knots. In number theory, the Legendre symbol, plays a similar role thanks to quadratic reciprocity

and hence we can view the Legendre symbol as indicating whether the knots corresponding to different primes are linked or not. Whereas it is natural in knot theory to investigate whether collections of 3, 4 or 27 knots are intricately linked (or not), few people would consider the problem whether one collection of 27 primes differs from another set of 27 primes worthy of investigation.

There’s one noteworthy exception, the Redei symbol which we can now view as giving information about the link-behavior of the knots associated to three different primes. For example, one can hunt for prime-triples whose knots link as the Borromean rings

(note that the knots corresponding to the three primes are not the unknot but more complicated). Here’s where the story gets interesting : in number-theory one would like to discover ‘higher reciprocity laws’ (for collections of n prime numbers) by imitating higher-link invariants in knot-theory. This should be done by trying to correspond filtrations on the fundamental group of the knot-complement to that of the algebraic fundamental group of $Spec(\mathbb{Z})-{ p } $ This project is called arithmetic topology

Perhaps I should make a pod- or vod-cast of that 20 minute talk, one day…

6 Comments