Skip to content →

Tag: symmetry

icosahedral group

Published October 21, 2004 by lievenlb

In my geometry 101 course I'm doing the rotation-symmetry groups
of the Platonic solids right now. This goes slightly slower than
expected as it turned out that some secondary schools no longer give a
formal definition of what a group is. So, a lot of time is taken up
explaining permutations and their properties as I want to view the
Platonic groups as subgroups of the permutation groups on the vertices.
To prove that the _tetrahedral group_ is isomorphic to $A_4$ was pretty
straigthforward and I'm half way through proving that the
_octahedral group_ is just $S_4$ (using the duality of the octahedron
with the cube and using the $4$ body diagonals of the cube).
Next
week I have to show that the _icosahedral group_ is isomorphic to $A_5$
which is a lot harder. The usual proof (that is, using the duality
between the icosahedron and the dodecahedron and using the $5$ cubes
contained in the dodecahedron, one for each of the diagonals of a face)
involves too much calculations to do in one hour. An alternative road is
to view the icosahedral group as a subgroup of $S_6$ (using the main
diagonals on the $12$ vertices of the icosahedron) and identifying this
subgroup as $A_5$. A neat exposition of this approach is given by John Baez in his
post Some thoughts on
the number $6$. (He also has another post on the icosahedral group
in his Week 79's
finds in mathematical physics).

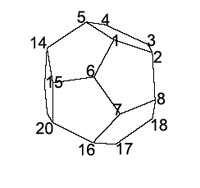But
probably I'll go for an “In Gap we
thrust”-argument. Using the numbers on the left, the rotation by
$72^o$ counter-clockwise in the top face we get the permutation in
$S_{20}$
$(1,2,3,4,5)(6,8,10,12,14)(7,9,11,13,15)(16,17,18,19,20)$
and the
rotation by $72^o$ counterclockwise along the face $(1,2,8,7,8)$ gives
the permutation
$(1,6,7,8,2)(3,5,15,16,9)(4,14,20,17,10)(12,13,19,18,11)$
GAP
calculates that the subgroup $dode$ of $S_{20}$ generated by these two
elements is $60$ (the correct number) and with $IsSimplegroup(dode);$ we
find that this group must be simple. Finally using
$IsomorphismTypeInfoFiniteSimplegroup(dode);$
we get the required
result that the group is indeed isomorphic to $A_5$. The time saved I
can then use to tell something about the classification project of
finite simple groups which might be more inspiring than tedious
calculations…

Leave a Comment

a cosmic Galois group

Published October 6, 2004 by lievenlb

Are
there hidden relations between mathematical and physical constants such
as

$\frac{e^2}{4 \pi \epsilon_0 h c} \sim \frac{1}{137} $

or are these numerical relations mere accidents? A couple of years
ago, Pierre Cartier proposed in his paper A mad day’s work : from Grothendieck to Connes and
Kontsevich : the evolution of concepts of space and symmetry that
there are many reasons to believe in a cosmic Galois group acting on the
fundamental constants of physical theories and responsible for relations
such as the one above.

The Euler-Zagier numbers are infinite
sums over $n_1 > n_2 > ! > n_r \geq 1 $ of the form

$\zeta(k_1,\dots,k_r) = \sum n_1^{-k_1} \dots n_r^{-k_r} $

and there are polynomial relations with rational coefficients between
these such as the product relation

$\zeta(a)\zeta(b)=\zeta(a+b)+\zeta(a,b)+\zeta(b,a) $

It is
conjectured that all polynomial relations among Euler-Zagier numbers are
consequences of these product relations and similar explicitly known
formulas. A consequence of this conjecture would be that
$\zeta(3),\zeta(5),\dots $ are all trancendental!

Drinfeld
introduced the Grothendieck-Teichmuller group-scheme over $\mathbb{Q} $
whose Lie algebra $\mathfrak{grt}_1 $ is conjectured to be the free Lie
algebra on infinitely many generators which correspond in a natural way
to the numbers $\zeta(3),\zeta(5),\dots $. The Grothendieck-Teichmuller
group itself plays the role of the Galois group for the Euler-Zagier
numbers as it is conjectured to act by automorphisms on the graded
$\mathbb{Q} $-algebra whose degree $d $-term are the linear combinations
of the numbers $\zeta(k_1,\dots,k_r) $ with rational coefficients and
such that $k_1+\dots+k_r=d $.

The Grothendieck-Teichmuller
group also appears mysteriously in non-commutative geometry. For
example, the set of all Kontsevich deformation quantizations has a
symmetry group which Kontsevich conjectures to be isomorphic to the
Grothendieck-Teichmuller group. See section 4 of his paper Operads and motives in
deformation quantzation for more details.

It also appears
in the renormalization results of Alain Connes and Dirk Kreimer. A very
readable introduction to this is given by Alain Connes himself in Symmetries Galoisiennes
et renormalisation. Perhaps the latest news on Cartier’s dream of a
cosmic Galois group is the paper by Alain Connes and Matilde Marcolli posted
last month on the arXiv : Renormalization and
motivic Galois theory. A good web-page on all of this, including
references, can be found here.

Leave a Comment

explaining symmetry

Published September 10, 2004 by lievenlb


PseudonomousDaughterTwo learned vector-addition at school and
important formulas such as the _Chasles-Moebius_ equation

$\forall A,B,C \in \mathbb{R}^2~:~\vec{AB}+\vec{BC} = \vec{AC} $

Last evening I helped her a bit with her homework and there was one
problem she could not do immediately (but it was a starred exercise so
you didn't have to do it, but…) :

consider a regular pentagon
with center $\vec{0} $. Prove that

$\vec{0A} + \vec{0B} +
\vec{0C} + \vec{0D} + \vec{0E} = \vec{0} $

PD2 : How would
_you_ do this? (with a tone like : I bet even you can't do
it)
Me : Symmetry!
PD2 : Huh?
Me : Rotate the plane
1/5 turn, then $A \mapsto B $, $B \mapsto C $ and so on. So the vector
giving the sum of all five terms must be mapped to itself under this
rotation and the only vector doing this is the zero vector.
PD2 :
That cannot be the solution, you didn't take sums of vectors and all
other exercises did that.
Me : I don't care, it is an elegant
solution, you don't have to compute a thing!

But clearly
she was not convinced and I had to admit there was nothing in her
textbook preparing her for such an argument. I was about to explain that
there was even more symmetry : reflecting along a line through a vertex
giving dihedral symmetry when I saw what the _intended solution_
of the exercise was :

Me : Okay, if you _have_ to do
sums let us try this. Fix a vertex, say A. Then the sum
$\vec{0E}+\vec{0B} $ must lie on the line 0A by the parallellogram-rule
(always good to drop in a word from the textbook to gain some
trust…), similarly the sum $\vec{0C}+\vec{0D} $ must lie on the
line 0A. So you now have to do a sum of three vectors lying on the
line 0A so the result must lie on 0A
PD2 : Yes, and???
Me : But there was nothing special about $A$. I could have started with
B and do the whole argument all over again and then I would get that
the sum is a vector on the line 0B
PD2 : And the only vector
lying on both 0A and 0B is $\vec{0} $
Me : Right! But
all we did now was just redoing the symmetry argument because the line
0A is mapped to 0B
PD2 : Don't you get started on
_that symmetry_ again!

I wonder which of the two
solutions she will sell today as her own. I would love to see the face
of a teacher when a 15yr old says “Clearly that is trivial because
the zero vector is the only one left invariant under
pentagon-symmetry!”

Leave a Comment