Skip to content →

Tag: Roubaud

On categories, go and the book $\in$

Published July 24, 2014 by lievenlb

A nice interview with Jacques Roubaud (the guy responsible for Bourbaki’s death announcement) in the courtyard of the ENS. He talks about go, categories, the composition of his book $\in$ and, of course, Grothendieck and Bourbaki.

Clearly there are pop-math books like dedicated to $\pi$ or $e$, but I don’t know just one novel having as its title a single mathematical symbol : $\in$ by Jacques Roubaud, which appeared in 1967.

The book consists of 361 small texts, 180 for the white stones and 181 for the black stones in a game of go, between Masami Shinohara (8th dan) and Mitsuo Takei (2nd Kyu). Here’s the game:

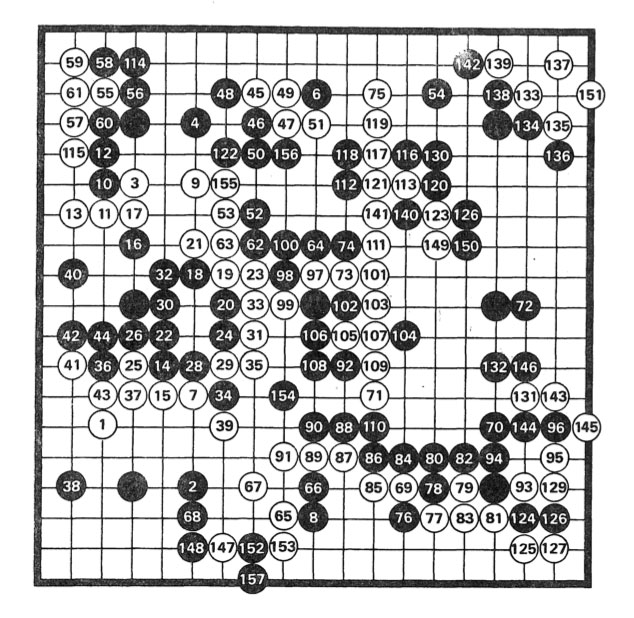
In the interview, Roubaud tells that go became quite popular in the mid sixties among French mathematicians, or at least those in the circle of Chevalley, who discovered the game in Japan and became a go-envangelist on his return to Paris.

In the preface to $\in$, the reader is invited to read it in a variety of possible ways. Either by paying attention to certain groupings of stones on the board, the corresponding texts sharing a common theme. Or, by reading them in order of how the go-game evolved (the numbering of white and black stones is not the same as the texts appearing in the book, fortunately there’s a conversion table on pages 153-155).

Or you can read them by paragraph, and each paragraph has as its title a mathematical symbol. We have $\in$, $\supset$, $\Box$, Hilbert’s $\tau$ and an imagined symbol ‘Symbole de la réflexion’, which are two mirrored and overlapping $\in$’s. For more information, thereader should consult the “Dictionnaire de la langue mathématique” by Lachatre and … Grothendieck.

According to the ‘bibliographie’ below it is number 17 in the ‘Publications of the L.I.T’.

Other ‘odd’ books in the list are: Bourbaki’s book on set theory, the thesis of Jean Benabou (who is responsible for Roubaud’s conversion from solving the exercises in Bourbaki to doing work in category theory. Roubaud also claims in the interview that category theory inspired him in the composition of the book $\in$) and there’s also Guillaume d’Ockham’s ‘Summa logicae’…

Leave a Comment

Oulipo’s use of the Tohoku paper

Published July 17, 2014 by lievenlb

Many identify the ‘Tohoku Mathematical Journal’ with just one paper published in it, affectionately called the Tohoku paper: “Sur quelques points d’algèbre homologique” by Alexander Grothendieck.

In this paper, Grothendieck reshaped homological algebra for Abelian categories, extending the setting of Cartan-Eilenberg (their book and the paper both appeared in 1957). While working on the Tohoku paper in Kansas, Grothendieck did not have access to the manuscript of the 1956 book of Cartan-Eilenberg, about which he heard from his correspondence with Serre.

Concerning the title, an interesting suggestion was made by Mathieu Bélanger in his thesis “Grothendieck et les topos: rupture et continuité dans les modes d’analyse du concept d’espace topologique”, (footnote 18 on page 164):

“There is a striking resemblance between the title of the Grothendieck’s article “Sur quelques points d’algèbre homologique”, and that of Fréchet‘s thesis “Sur quelques points d’analyse fonctionelle”. Why? Grothendieck remains silent about it. Perhaps he saw a methodological similarity between the introduction, by Fréchet, of abstract spaces in order to develop the foundations of functional calculus and that of the Abelian categories he needed to clarify the homological theory. Compared with categories of sets, groups, topological spaces, etc. that were used until then, Abelian categories are in effect abstract categories.”

But, what does this have to do with the literary group OuLiPo (ouvroir de littérature potentielle, ‘workshop of potential literature’)?

Oulipo was founded in 1960 by Raymond Queneau and François Le Lionnais. Other notable members have included novelists Georges Perec and Italo Calvino, poets Oskar Pastior, Jean Lescure and poet/mathematician Jacques Roubaud.

Several members of Oulipo were either active mathematicians or at least had an interest in mathematics. Sometimes, Oulipo is said to be the literary answer to Bourbaki. The group explored new ways to create literature, often with methods coming from mathematics or programming.

One such method is described in “Chimères” by Le Lionnais:

One takes a source text A. One ’empties’ it, that is, one deletes all nouns, adjectives and verbs, but marks where they were in the text. In this way we have ‘prepared’ the text.

Next we take three target texts and make lists of words from them, K the list of nouns of the first, L the list of adjectives of the second and M the list of verbs of the third. Finally, we fill the empty spaces in the source text by words from the target lists, in the order that they appeared in the target texts.

In the example Le Lionnais gives, the liste M is the list of all verbs appearing in the Tohoku paper.


Leave a Comment

Grothendieck’s Café

Published July 1, 2014 by lievenlb

“A story says that in a Paris café around 1955 Grothendieck asked his friends “what is a scheme?”. At the time only an undefined idea of “schéma” was current in Paris, meaning more or less whatever would improve on Weil’s foundations.” (McLarty in The Rising Sea)

Finding that particular café in Paris, presumably in the 5th arrondissement, seemed like looking for a needle in a haystack.

Until now.

In trying to solve the next riddle in Bourbaki’s death announcement:

A reception will be held at the Bar ‘The Direct Products’, at the crossroads of the Projective Resolutions (formerly Koszul square)

I’ve been reading Mathematics, a novel by Jacques Roubaud (the guy responsible for the announcement) on Parisian math-life in the 50ties and 60ties.

It turns out that the poor Bourbakistas had very little choice if they wanted to have a beer (or coffee) after attending a seminar at the IHP.

On page 114, Roubaud writes:

“Père Plantin presided over his bar, which presided over the Lhomond/Ulm street corner. It is an obvious choice. rue Pierre-et-Marie-Curie had no bars; rue d’Ulm had no bars in eyeshot either. If we emerged, as we did, on this side of the Institut Henri Poincaré (for doing so on the other side would have meant fraternizing with the Spanish and Geography students in the cafés on rue Saint-Jacques, which was out of the question), we had no choice. Café Plantin had a hegemony.”

It is unclear to me whether Plantin was once actually the name of the café, or that it’s just Roubaud’s code-word for it. At other places in the book, e.g. on pages 82 and 113, he consistently writes “Plantin”, between quotes.

Today, the café on the crossroads of rue d’Ulm (where the Ecole Normal Superieure is located) and de rue Lhomond is the Interlude Café

and here’s what Roubaud has to say about it, or rather about the situation in 1997, when the French version of his book was published:

“the thing that would currently be found at the very same corner of rues Lhomond/Ulm would not be what I am here terming “Plantin”.”

So, we can only hope that the Café ‘Aux Produits Directs’ was a lot cosier, way back then.

But let us return to Grothendieck’s “What is a scheme?” story.

Now that we have a fair idea of location, what about a possible date? Here’s a suggestion: this happened on monday december 12th, 1955, and, one of the friends present must have been Cartier.

Here’s why.

The very first time the word “schéma” was uttered, in Paris, at an official seminar talk, was during the Cartan seminar of 1955/56 on algebraic geometry.

The lecturer was Claude Chevalley, and the date was december 12th 1955.


I’m fairly certain Grothendieck and Cartier attended and that Cartier was either briefed before or understood the stuff at once (btw. he gave another talk on schemes, a year later at the Chevalley seminar).

A couple of days later, on december 15th, Grothendieck sends a letter to his pal Serre (who must have been out of Paris for otherwise they’d phone each other) ending with:



Note the phrase: I am exploiting him most profitably. Yes, by asking him daft questions over a pint at Café “Plantin”…

Leave a Comment