Tag: representations

permutation representations of monodromy groups

Published March 20, 2007 by lievenlb

Today we will explain how curves defined over
$\overline{\mathbb{Q}} $ determine permutation representations
of the carthographic groups. We have seen that any smooth projective
curve $C $ (a Riemann surface) defined over the algebraic
closure $\overline{\mathbb{Q}} $ of the rationals, defines a
_Belyi map_ $\xymatrix{C \ar[rr]^{\pi} & & \mathbb{P}^1} $ which is only ramified over the three points
$\\{ 0,1,\infty \\} $. By this we mean that there are
exactly $d $ points of $C $ lying over any other point
of $\mathbb{P}^1 $ (we call $d $ the degree of
$\pi $) and that the number of points over $~0,1~ $ and
$~\infty $ is smaller than $~d $. To such a map we
associate a _dessin d\’enfant_, a drawing on $C $ linking the
pre-images of $~0 $ and $~1 $ with exactly $d $
edges (the preimages of the open unit-interval). Next, we look at
the preimages of $~0 $ and associate a permutation
$\tau_0 $ of $~d $ letters to it by cycling
counter-clockwise around these preimages and recording the edges we
meet. We repeat this procedure for the preimages of $~1 $ and
get another permutation $~\tau_1 $. That is, we obtain a
subgroup of the symmetric group $ \langle \tau_0,\tau_1
\rangle \subset S_d $ which is called the monodromy
group of the covering $\pi $.

For example, the
dessin on the right is
associated to a degree $8 $ map $\mathbb{P}^1 \rightarrow
\mathbb{P}^1 $ and if we let the black (resp. starred) vertices be
the preimages of $~0 $ (respectively of $~1 $), then the
corresponding partitions are $\tau_0 = (2,3)(1,4,5,6) $
and $\tau_1 = (1,2,3)(5,7,8) $ and the monodromy group
is the alternating group $A_8 $ (use
GAP ).

But wait! The map is also
ramified in $\infty $ so why don\’t we record also a
permutation $\tau_{\infty} $ and are able to compute it from
the dessin? (Note that all three partitions are needed if we want to
reconstruct $C $ from the $~d $ sheets as they encode in
which order the sheets fit together around the preimages). Well,
the monodromy group of a $\mathbb{P}^1 $ covering ramified only
in three points is an epimorphic image of the fundamental
group of the sphere
minus three points $\pi_1(\mathbb{P}^1 – { 0,1,\infty
}) $ That is, the group of all loops beginning and
ending in a basepoint upto homotopy (that is, two such loops are the
same if they can be transformed into each other in a continuous way
while avoiding the three points).

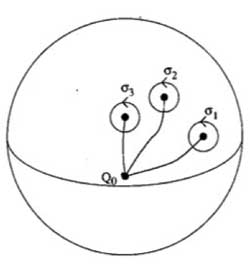This group is generated by loops
$\sigma_i $ running from the basepoint to nearby the i-th
point, doing a counter-clockwise walk around it and going back to be
basepoint $Q_0 $ and the epimorphism to the monodromy group is given by sending

$\sigma_1 \mapsto \tau_0~\quad~\sigma_2 \mapsto
\tau_1~\quad~\sigma_3 \mapsto \tau_{\infty} $

Now,
these three generators are not independent. In fact, this fundamental
group is

$\pi_1(\mathbb{P}^1 – \\{ 0,1,\infty \\}) =
\langle \sigma_1,\sigma_2,\sigma_3~\mid~\sigma_1 \sigma_2
\sigma_3 = 1 \rangle $

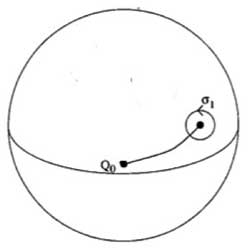To understand this, let us begin
with an easier case, that of the sphere minus one point. The fundamental group of the plane minus one point is
$~\mathbb{Z} $ as it encodes how many times we walk around the
point. However, on the sphere the situation is different as we can make
our walk around the point longer and longer until the whole walk is done
at the backside of the sphere and then we can just contract our walk to
the basepoint. So, there is just one type of walk on a sphere minus one
point (upto homotopy) whence this fundamental group is trivial. Next,
let us consider the sphere minus two points

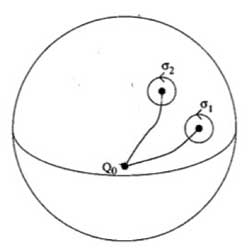
Repeat the foregoing to the walk $\sigma_2 $, that
is, strech the upper part of the circular tour all over the backside of
the sphere and then we see that we can move it to fit with the walk
$\sigma_1$ BUT for the orientation of the walk! That is, if we do this
modified walk $\sigma_1 \sigma_2^{\’} $ we just made the
trivial walk. So, this fundamental group is $\langle
\sigma_1,\sigma_2~\mid~\sigma_1 \sigma_2 = 1 \rangle =
\mathbb{Z} $ This is also the proof of the above claim. For,
we can modify the third walk $\sigma_3 $ continuously so that
it becomes the walk $\sigma_1 \sigma_2 $ but
with the reversed orientation ! As $\sigma_3 =
(\sigma_1 \sigma_2)^{-1} $ this allows us to compute the
\’missing\’ permutation $\tau_{\infty} = (\tau_0
\tau_1)^{-1} $ In the example above, we obtain
$\tau_{\infty}= (1,2,6,5,8,7,4)(3) $ so it has two cycles
corresponding to the fact that the dessin has two regions (remember we
should draw ths on the sphere) : the head and the outer-region. Hence,
the pre-images of $\infty$ correspond to the different regions of the
dessin on the curve $C $. For another example,
consider the degree 168 map

$K \rightarrow \mathbb{P}^1 $

which is the modified orbit map for the action of
$PSL_2(\mathbb{F}_7) $ on the Klein quartic.
The corresponding dessin is the heptagonal construction of the Klein
quartic

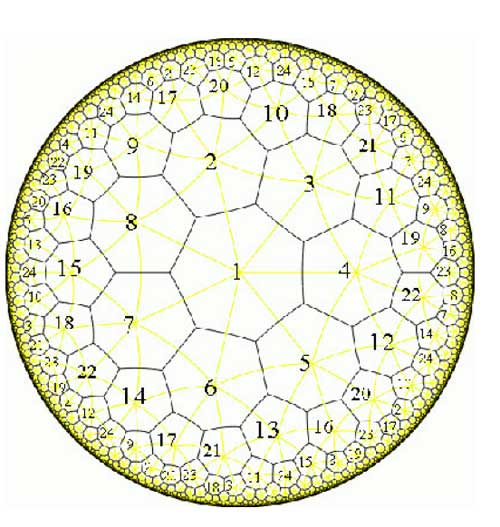
Here, the pre-images of 1 correspond to the midpoints of the
84 edges of the polytope whereas the pre-images of 0 correspond to the
56 vertices. We can label the 168 half-edges by numbers such that
$\tau_0 $ and $\tau_1 $ are the standard generators b
resp. a of the 168-dimensional regular representation (see the atlas
page ).
Calculating with GAP the element $\tau_{\infty} = (\tau_0
\tau_1)^{-1} = (ba)^{-1} $ one finds that this permutation
consists of 24 cycles of length 7, so again, the pre-images of
$\infty $ lie one in each of the 24 heptagonal regions of the
Klein quartic. Now, we are in a position to relate curves defined
over $\overline{Q} $ via their Belyi-maps and corresponding
dessins to Grothendiecks carthographic groups $\Gamma(2) $,
$\Gamma_0(2) $ and $SL_2(\mathbb{Z}) $. The
dessin gives a permutation representation of the monodromy group and
because the fundamental group of the sphere minus three
points $\pi_1(\mathbb{P}^1 – \\{ 0,1,\infty \\}) =
\langle \sigma_1,\sigma_2,\sigma_3~\mid~\sigma_1 \sigma_2
\sigma_3 = 1 \rangle = \langle \sigma_1,\sigma_2
\rangle $ is the free group op two generators, we see that
any dessin determines a permutation representation of the congruence
subgroup $\Gamma(2) $ (see this
post where we proved that this
group is free). A clean dessin is one for which one type of
vertex has all its valancies (the number of edges in the dessin meeting
the vertex) equal to one or two. (for example, the pre-images of 1 in
the Klein quartic-dessin or the pre-images of 1 in the monsieur Mathieu
example ) The corresponding
permutation $\tau_1 $ then consists of 2-cycles and hence the
monodromy group gives a permutation representation of the free
product $C_{\infty} \ast C_2 =
\Gamma_0(2) $ Finally, a clean dessin is said to be a
quilt dessin if also the other type of vertex has all its valancies
equal to one or three (as in the Klein quartic or Mathieu examples).
Then, the corresponding permutation has order 3 and for these
quilt-dessins the monodromy group gives a permutation representation of
the free product $C_2 \ast C_3 =
PSL_2(\mathbb{Z}) $ Next time we will see how this lead
Grothendieck to his anabelian geometric approach to the absolute Galois
group.

One Comment

noncommutative curves and their maniflds

Published March 17, 2007 by lievenlb

Last time we have
seen that the noncommutative manifold of a Riemann surface can be viewed
as that Riemann surface together with a loop in each point. The extra
loop-structure tells us that all finite dimensional representations of
the coordinate ring can be found by separating over points and those
living at just one point are classified by the isoclasses of nilpotent
matrices, that is are parametrized by the partitions (corresponding
to the sizes of the Jordan blocks). In addition, these loops tell us
that the Riemann surface locally looks like a Riemann sphere, so an
equivalent mental picture of the local structure of this
noncommutative manifold is given by the picture on teh left, where the surface is part of the Riemann surface
and a sphere is placed at every point. Today we will consider
genuine noncommutative curves and describe their corresponding
noncommutative manifolds.

Here, a mental picture of such a
_noncommutative sphere_ to keep in mind would be something
like the picture on the right. That is, in most points of the sphere we place as before again
a Riemann sphere but in a finite number of points a different phenomen
occurs : we get a cluster of infinitesimally nearby points. We
will explain this picture with an easy example. Consider the
complex plane $\mathbb{C} $, the points of which are just the
one-dimensional representations of the polynomial algebra in one
variable $\mathbb{C}[z] $ (any algebra map $\mathbb{C}[z] \rightarrow \mathbb{C} $ is fully determined by the image of z). On this plane we
have an automorphism of order two sending a complex number z to its
negative -z (so this automorphism can be seen as a point-reflexion
with center the zero element 0). This automorphism extends to
the polynomial algebra, again induced by sending z to -z. That
is, the image of a polynomial $f(z) \in \mathbb{C}[z] $ under this
automorphism is f(-z).

With this data we can form a noncommutative
algebra, the _skew-group algebra_ $\mathbb{C}[z] \ast C_2 $ the
elements of which are either of the form $f(z) \ast e $ or $g(z) \ast g $ where
$C_2 = \langle g : g^2=e \rangle $ is the cyclic group of order two
generated by the automorphism g and f(z),g(z) are arbitrary
polynomials in z.

The multiplication on this algebra is determined by
the following rules

$(g(z) \ast g)(f(z) \ast e) = g(z)f(-z) \astg $ whereas $(f(z) \ast e)(g(z) \ast g) = f(z)g(z) \ast g $

$(f(z) \ast e)(g(z) \ast e) = f(z)g(z) \ast e $ whereas $(f(z) \ast g)(g(z)\ast g) = f(z)g(-z) \ast e $

That is, multiplication in the
$\mathbb{C}[z] $ factor is the usual multiplication, multiplication in
the $C_2 $ factor is the usual group-multiplication but when we want
to get a polynomial from right to left over a group-element we have to
apply the corresponding automorphism to the polynomial (thats why we
call it a _skew_ group-algebra).

Alternatively, remark that as
a $\mathbb{C} $-algebra the skew-group algebra $\mathbb{C}[z] \ast C_2 $ is
an algebra with unit element 1 = 1\aste and is generated by
the elements $X = z \ast e $ and $Y = 1 \ast g $ and that the defining
relations of the multiplication are

$Y^2 = 1 $ and $Y.X =-X.Y $

hence another description would
be

$\mathbb{C}[z] \ast C_2 = \frac{\mathbb{C} \langle X,Y \rangle}{ (Y^2-1,XY+YX) } $

It can be shown that skew-group
algebras over the coordinate ring of smooth curves are _noncommutative
smooth algebras_ whence there is a noncommutative manifold associated
to them. Recall from last time the noncommutative manifold of a
smooth algebra A is a device to classify all finite dimensional
representations of A upto isomorphism Let us therefore try to
determine some of these representations, starting with the
one-dimensional ones, that is, algebra maps from

$\mathbb{C}[z] \ast C_2 = \frac{\mathbb{C} \langle X,Y \rangle}{ (Y^2-1,XY+YX) } \rightarrow \mathbb{C} $

Such a map is determined by the image of X and that of
Y. Now, as $Y^2=1 $ we have just two choices for the image of Y
namely +1 or -1. But then, as the image is a commutative algebra
and as XY+YX=0 we must have that the image of 2XY is zero whence the
image of X must be zero. That is, we have only
two one-dimensional representations, namely $S_+ : X \rightarrow 0, Y \rightarrow 1 $
and $S_- : X \rightarrow 0, Y \rightarrow -1 $

This is odd! Can
it be that our noncommutative manifold has just 2 points? Of course not.
In fact, these two points are the exceptional ones giving us a cluster
of nearby points (see below) whereas most points of our
noncommutative manifold will correspond to 2-dimensional
representations!

So, let’s hunt them down. The
center of $\mathbb{C}[z]\ast C_2 $ (that is, the elements commuting with
all others) consists of all elements of the form $f(z)\ast e $ with f an
_even_ polynomial, that is, f(z)=f(-z) (because it has to commute
with 1\ast g), so is equal to the subalgebra $\mathbb{C}[z^2]\ast e $.

The
manifold corresponding to this subring is again the complex plane
$\mathbb{C} $ of which the points correspond to all one-dimensional
representations of $\mathbb{C}[z^2]\ast e $ (determined by the image of
$z^2\ast e $).

We will now show that to each point of $\mathbb{C} – { 0 } $
corresponds a simple 2-dimensional representation of
$\mathbb{C}[z]\ast C_2 $.

If a is not zero, we will consider the
quotient of the skew-group algebra modulo the twosided ideal generated
by $z^2\ast e-a $. It turns out
that

$\frac{\mathbb{C}[z]\ast C_2}{(z^2\aste-a)} =
\frac{\mathbb{C}[z]}{(z^2-a)} \ast C_2 = (\frac{\mathbb{C}[z]}{(z-\sqrt{a})}
\oplus \frac{\mathbb{C}[z]}{(z+\sqrt{a})}) \ast C_2 = (\mathbb{C}
\oplus \mathbb{C}) \ast C_2 $

where the skew-group algebra on the
right is given by the automorphism g on $\mathbb{C} \oplus \mathbb{C} $ interchanging the two factors. If you want to
become more familiar with working in skew-group algebras work out the
details of the fact that there is an algebra-isomorphism between
$(\mathbb{C} \oplus \mathbb{C}) \ast C_2 $ and the algebra of $2 \times 2 $ matrices $M_2(\mathbb{C}) $. Here is the
identification

$~(1,0)\aste \rightarrow \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} $

$~(0,1)\aste \rightarrow \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} $

$~(1,0)\astg \rightarrow \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} $

$~(0,1)\astg \rightarrow \begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} $

so you have to verify that multiplication
on the left hand side (that is in $(\mathbb{C} \oplus \mathbb{C}) \ast
C_2 $) coincides with matrix-multiplication of the associated
matrices.

Okay, this begins to look like what we are after. To
every point of the complex plane minus zero (or to every point of the
Riemann sphere minus the two points ${ 0,\infty } $) we have
associated a two-dimensional simple representation of the skew-group
algebra (btw. simple means that the matrices determined by the images
of X and Y generate the whole matrix-algebra).

In fact, we
now have already classified ‘most’ of the finite dimensional
representations of $\mathbb{C}[z]\ast C_2 $, namely those n-dimensional
representations

$\mathbb{C}[z]\ast C_2 =
\frac{\mathbb{C} \langle X,Y \rangle}{(Y^2-1,XY+YX)} \rightarrow M_n(\mathbb{C}) $

for which the image of X is an invertible $n \times n $ matrix. We can show that such representations only exist when
n is an even number, say n=2m and that any such representation is
again determined by the geometric/combinatorial data we found last time
for a Riemann surface.

That is, It is determined by a finite
number ${ P_1,\dots,P_k } $ of points from $\mathbb{C} – 0 $ where
k is at most m. For each index i we have a positive
number $a_i $ such that $a_1+\dots+a_k=m $ and finally for each i we
also have a partition of $a_i $.

That is our noncommutative
manifold looks like all points of $\mathbb{C}-0 $ with one loop in each
point. However, we have to remember that each point now determines a
simple 2-dimensional representation and that in order to get all
finite dimensional representations with det(X) non-zero we have to
scale up representations of $\mathbb{C}[z^2] $ by a factor two.
The technical term here is that of a Morita equivalence (or that the
noncommutative algebra is an Azumaya algebra over
$\mathbb{C}-0 $).

What about the remaining representations, that
is, those for which Det(X)=0? We have already seen that there are two
1-dimensional representations $S_+ $ and $S_- $ lying over 0, so how
do they fit in our noncommutative manifold? Should we consider them as
two points and draw also a loop in each of them or do we have to do
something different? Rememer that drawing a loop means in our
geometry -> representation dictionary that the representations
living at that point are classified in the same way as nilpotent
matrices.

Hence, drawing a loop in $S_+ $ would mean that we have a
2-dimensional representation of $\mathbb{C}[z]\ast C_2 $ (different from
$S_+ \oplus S_+ $) and any such representation must correspond to
matrices

$X \rightarrow \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} $ and $Y \rightarrow \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} $

But this is not possible as these matrices do
_not_ satisfy the relation XY+YX=0. Hence, there is no loop in $S_+ $
and similarly also no loop in $S_- $.

However, there are non
semi-simple two dimensional representations build out of the simples
$S_+ $ and $S_- $. For, consider the matrices

$X \rightarrow \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} $ and $Y \rightarrow \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} $

then these
matrices _do_ satisfy XY+YX=0! (and there is another matrix-pair
interchanging $\pm 1 $ in the Y-matrix). In erudite terminology this
says that there is a _nontrivial extension_ between $S_+ $ and $S_- $
and one between $S_- $ and $S_+ $.

In our dictionary we will encode this
information by the picture

$\xymatrix{\vtx{}
\ar@/^2ex/[rr] & & \vtx{} \ar@/^2ex/[ll]} $

where the two
vertices correspond to the points $S_+ $ and $S_- $ and the arrows
represent the observed extensions. In fact, this data suffices to finish
our classification project of finite dimensional representations of
the noncommutative curve $\mathbb{C}[z] \ast C_2 $.

Those with Det(X)=0
are of the form : $R \oplus T $ where R is a representation with
invertible X-matrix (which we classified before) and T is a direct
sum of representations involving only the simple factors $S_+ $ and
$S_- $ and obtained by iterating the 2-dimensional idea. That is, for
each factor the Y-matrix has alternating $\pm 1 $ along the diagonal
and the X-matrix is the full nilpotent Jordan-matrix.

So
here is our picture of the noncommutative manifold of the
noncommutative curve $\mathbb{C}[z]\ast C_2 $ : the points are all points
of $\mathbb{C}-0 $ together with one loop in each of them together
with two points lying over 0 where we draw the above picture of arrows
between them. One should view these two points as lying
infinetesimally close to each other and the gluing
data

$\xymatrix{\vtx{} \ar@/^2ex/[rr] & & \vtx{}
\ar@/^2ex/[ll]} $

contains enough information to determine
that all other points of the noncommutative manifold in the vicinity of
this cluster should be two dimensional simples! The methods used
in this simple minded example are strong enough to determine the
structure of the noncommutative manifold of _any_ noncommutative curve.

So, let us look at a real-life example. Once again, take the
Kleinian quartic In a previous
course-post we recalled that
there is an action by automorphisms on the Klein quartic K by the
finite simple group $PSL_2(\mathbb{F}_7) $ of order 168. Hence, we
can form the noncommutative Klein-quartic $K \ast PSL_2(\mathbb{F}_7) $
(take affine pieces consisting of complements of orbits and do the
skew-group algebra construction on them and then glue these pieces
together again).

We have also seen that the orbits are classified
under a Belyi-map $K \rightarrow \mathbb{P}^1_{\mathbb{C}} $ and that this map
had the property that over any point of $\mathbb{P}^1_{\mathbb{C}}
– { 0,1,\infty } $ there is an orbit consisting of 168 points
whereas over 0 (resp. 1 and $\infty $) there is an orbit
consisting of 56 (resp. 84 and 24 points).

So what is
the noncommutative manifold associated to the noncommutative Kleinian?
Well, it looks like the picture we had at the start of this
post For all but three points of the Riemann sphere
$\mathbb{P}^1 – { 0,1,\infty } $ we have one point and one loop
(corresponding to a simple 168-dimensional representation of $K \ast
PSL_2(\mathbb{F}_7) $) together with clusters of infinitesimally nearby
points lying over 0,1 and $\infty $ (the cluster over 0
is depicted, the two others only indicated).

Over 0 we have
three points connected by the diagram

$\xymatrix{& \vtx{} \ar[ddl] & \\ & & \\ \vtx{} \ar[rr] & & \vtx{} \ar[uul]} $

where each of the vertices corresponds to a
simple 56-dimensional representation. Over 1 we have a cluster of
two points corresponding to 84-dimensional simples and connected by
the picture we had in the $\mathbb{C}[z]\ast C_2 $ example).

Finally,
over $\infty $ we have the most interesting cluster, consisting of the
seven dwarfs (each corresponding to a simple representation of dimension
24) and connected to each other via the
picture

$\xymatrix{& & \vtx{} \ar[dll] & & \\ \vtx{} \ar[d] & & & & \vtx{} \ar[ull] \\ \vtx{} \ar[dr] & & & & \vtx{} \ar[u] \\ & \vtx{} \ar[rr] & & \vtx{} \ar[ur] &} $

Again, this noncommutative manifold gives us
all information needed to give a complete classification of all finite
dimensional $K \ast PSL_2(\mathbb{F}_7) $-representations. One
can prove that all exceptional clusters of points for a noncommutative
curve are connected by a cyclic quiver as the ones above. However, these
examples are still pretty tame (in more than one sense) as these
noncommutative algebras are finite over their centers, are Noetherian
etc. The situation will become a lot wilder when we come to exotic
situations such as the noncommutative manifold of
$SL_2(\mathbb{Z}) $…

One Comment

the noncommutative manifold of a Riemann surface

Published March 16, 2007 by lievenlb

The
natural habitat of this lesson is a bit further down the course, but it
was called into existence by a comment/question by
Kea

I don’t yet quite see where the nc
manifolds are, but I guess that’s coming.

As
I’m enjoying telling about all sorts of sources of finite dimensional
representations of $SL_2(\mathbb{Z}) $ (and will carry on doing so for
some time), more people may begin to wonder where I’m heading. For this
reason I’ll do a couple of very elementary posts on simple examples of
noncommutative manifolds.

I realize it is ‘bon ton’ these days
to say that noncommutative manifolds are virtual objects associated to
noncommutative algebras and that the calculation of certain invariants
of these algebras gives insight into the topology and/or geometry of
these non-existent spaces. My own attitude to noncommutative geometry is
different : to me, noncommutative manifolds are genuine sets of points
equipped with a topology and other structures which I can use as a
mnemotechnic device to solve the problem of interest to me which is the
classification of all finite dimensional representations of a smooth
noncommutative algebra.

Hence, when I speak of the
‘noncommutative manifold of $SL_2(\mathbb{Z}) $’ Im after an object
containing enough information to allow me (at least in principle) to
classify the isomorphism classes of all finite dimensional
$SL_2(\mathbb{Z}) $-representations. The whole point of this course is
to show that such an object exists and that we can make explicit
calculations with it. But I’m running far ahead. Let us start with
an elementary question :

Riemann surfaces are examples of
noncommutative manifolds, so what is the noncommutative picture of
them?

I’ve browsed the Google-pictures a bit and a picture
coming close to my mental image of the noncommutative manifold of a
Riemann surface locally looks like the picture on the left. Here, the checkerboard-surface is part of the Riemann surface
and the extra structure consists in putting in each point of the Riemann
surface a sphere, reflecting the local structure of the Riemann surface
near the point. In fact, my picture is slightly different : I want to
draw a loop in each point of the Riemann surface, but Ill explain why
the two pictures are equivalent and why they present a solution to the
problem of classifying all finite dimensional representations of the
Riemann surface. After all why do we draw and study Riemann
surfaces? Because we are interested in the solutions to equations. For
example, the points of the _Kleinian quartic Riemann
surface_ give us all solutions tex \in
\mathbb{C}^3 $ to the equation $X^3Y+Y^3Z+Z^3X=0 $. If (a,b,c) is such
a solution, then so are all scalar multiples $(\lambda a,\lambda
b,\lambda c) $ so we may as well assume that the Z$coordinate is equal
to 1 and are then interested in finding the solutions tex \in
\mathbb{C}^2 $ to the equation $X^3Y+Y^3+X=0 $ which gives us an affine
patch of the Kleinian quartic (in fact, these solutions give us all
points except for two, corresponding to the _points at infinity_ needed
to make the picture compact so that we can hold it in our hand and look
at it from all sides. These points at infinity correspond to the trivial
solutions (1,0,0) and (0,1,0)).

What is the connection
between points on this Riemann surface and representations? Well, if
(a,b) is a solution to the equation $X^3Y+Y^3+X=0 $, then we have a
_one-dimensional representation_ of the affine _coordinate ring_
$\mathbb{C}[X,Y]/(X^3Y+Y^3+X) $, that is, an algebra
morphism

$\mathbb{C}[X,Y]/(X^3Y+Y^3+X) \rightarrow \mathbb{C} $

defined by sending X to a and Y to b.
Conversely, any such one-dimensonal representation gives us a solution
(look at the images of X and Y and these will be the coordinates of
a solution). Thus, commutative algebraic geometry of smooth
curves (that is Riemann surfaces if you look at the ‘real’ picture)
can be seen as the study of one-dimensional representations of their
smooth coordinate algebras. In other words, the classical Riemann
surface gives us already the classifcation of all one-dimensional
representations, so now we are after the ‘other ones’.

In
noncommtative algebra it is not natural to restrict attention to algebra
maps to $\mathbb{C} $, at least we would also like to include algebra
maps to $n \times n $ matrices $M_n(\mathbb{C}) $. An n-dimensional
representation of the coordinate algebra of the Klein quartic is an
algebra map

$\mathbb{C}[X,Y]/(X^3Y+Y^3+X) \rightarrow M_n(\mathbb{C}) $

That is, we want to find all pairs of $n \times n $ matrices A and B satisfying the following
matrix-identities

$A.B=B.A $ and $A^3.B+B^3+A=0_n $

The
first equation tells us that the two matrices must commute (because we
took commuting variables X and Y) and the second equation really is
a set of $n^2 $-equations in the matrix-entries of A and
B.

There is a sneaky way to get lots of such matrix-couples
from a given solution (A,B), namely by _simultaneous conjugation_.
That is, if $C \in GL_n(\mathbb{C}) $ is any invertible $n \times n $
matrix, then also the matrix-couple $~(C^{-1}.A.C,C^{-1}.B.C) $
satisfies all the required equations (write the equations out and notice
that middle terms of the form $C.C^{-1} $ cancel out and check that one
then obtains the matrix-identities

$C^{-1} A B C = C^{-1} BA C $ and $C^{-1}(A^3B+B^3+A)C = 0_n $

which are satisfied because
(A,B) was supposed to be a solution). We then say that these two
n-dimensional representations are _isomorphic_ and naturally we are
only interested in classifying the isomorphism classes of all
representations.

Using classical commutative algebra theory of
Dedekind domains (such as the coordinate ring $\mathbb{C}[X,Y]/(X^3Y+Y^3+X) $)
allows us to give a complete solution to this problem. It says that any
n-dimensional representation is determined up to isomorphism by the
following geometric/combinatorial data

a finite set of points $P_1,P_2,\dots,P_k $ on the Riemann surface with $k \leq n $.
a set of positive integers $a_1,a_2,\dots,a_k $ associated to these pointssatisfying $a_1+a_2+\dots_a_k=n $.
for each $a_i $ a partition of $a_i $ (that is, a decreasing sequence of numbers with total sum
$a_i $).

To encode this classification I’ll use the mental
picture of associating to every point of the Klein quartic a small
loop. $\xymatrix{\vtx{}
\ar@(ul,ur)} $ Don\’t get over-exited about this
noncommutative manifold picture of the Klein quartic, I do not mean to
represent something like closed strings emanating from all points of the
Riemann surface or any other fanshi-wanshi interpretation. Just as
Feynman-diagrams allow the initiated to calculate probabilities of
certain interactions, the noncommutative manifold allows the
initiated to classify finite dimensional representations.

Our
mental picture of the noncommutative manifold of the Klein quartic, that
is : the points of the Klein quartic together with a loop in each point,
will tell the initiated quite a few things, such as : The fact
that there are no arrows between distict points, tells us that the
classification problem splits into local problems in a finite number of
points. Technically, this encodes the fact that there are no nontrivial
extensions between different simples in the commutative case. This will
drastically change if we enter the noncommutative world…

The fact that there is one loop in each point, tells us that
the local classification problem in that point is the same as that of
classifying nilpotent matrices upto conjugation (which, by the Jordan
normal form result, are classified by partitions) Moreover,
the fact that there is one loop in each point tells us that the local
structure of simple representations near that point (that is, the points
on the Kleinian quartic lying nearby) are classified as the simple
representations of the polynmial algebra $\mathbb{C}[x] $ (which are the
points on the complex plane, giving the picture
of the Riemann sphere in each point reflecting the local
neighborhood of the point on the Klein quartic)

In general, the
noncommutative manifold associated to a noncommutative smooth algebra
will be of a similar geometric/combinatorial nature. Typically, it will
consist of a geometric collection of points and arrows and loops between
these points. This data will then allow us to reduce the classification
problem to that of _quiver-representations_ and will allow us to give
local descriptions of our noncommutative manifolds. Next time,
I’ll give the details in the first noncommutative example : the
skew-group algebra of a finite group of automorphisms on a Riemann
surface (such as the simple group $PSL_2(\mathbb{F}_7) $ acting on the
Klein quartic). Already in this case, some new phenomena will
appear…

ADDED : While writing this post
NetNewsWire informed me that over at Noncommutative Geometry they have a
post on a similar topic : What is a noncommutative space.

One Comment