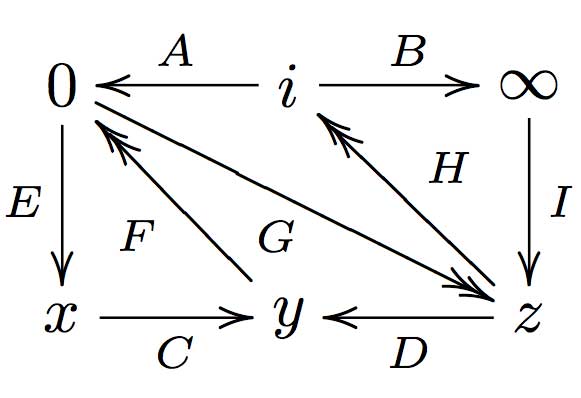
 We have associated to a subgroup of the modular group $PSL_2(\mathbb{Z}) $ a quiver (that is, an oriented graph). For example, one verifies that the fundamental domain of the subgroup $\Gamma_0(2) $ (an index 3 subgroup) is depicted on the right by the region between the thick lines with the identification of edges as indicated. The associated quiver is then
We have associated to a subgroup of the modular group $PSL_2(\mathbb{Z}) $ a quiver (that is, an oriented graph). For example, one verifies that the fundamental domain of the subgroup $\Gamma_0(2) $ (an index 3 subgroup) is depicted on the right by the region between the thick lines with the identification of edges as indicated. The associated quiver is then
\[
\xymatrix{i \ar[rr]^a \ar[dd]^b & & 1 \ar@/^/[ld]^h \ar@/_/[ld]_i \\
& \rho \ar@/^/[lu]^d \ar@/_/[lu]_e \ar[rd]^f & \\
0 \ar[ru]^g & & i+1 \ar[uu]^c}
\]
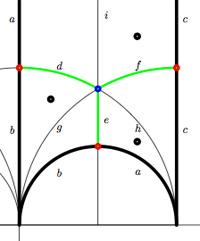
The corresponding “dessin d’enfant” are the green edges in the picture. But, the red dot on the left boundary is identied with the red dot on the lower circular boundary, so the dessin of the modular subgroup $\Gamma_0(2) $ is
\[
\xymatrix{| \ar@{-}[r] & \bullet \ar@{-}@/^8ex/[r] \ar@{-}@/_8ex/[r] & -}
\]
Here, the three red dots (all of them even points in the Dedekind tessellation) give (after the identification) the two points indicated by a $\mid $ whereas the blue dot (an odd point in the tessellation) is depicted by a $\bullet $. There is another ‘quiver-like’ picture associated to this dessin, a quilt of the modular subgroup $\Gamma_0(2) $ as studied by John Conway and Tim Hsu.
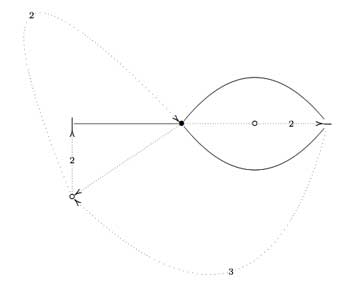 On the left, a quilt-diagram copied from Hsu’s book Quilts : central extensions, braid actions, and finite groups, exercise 3.3.9. This ‘quiver’ has also 5 vertices and 7 arrows as our quiver above, so is there a connection?
On the left, a quilt-diagram copied from Hsu’s book Quilts : central extensions, braid actions, and finite groups, exercise 3.3.9. This ‘quiver’ has also 5 vertices and 7 arrows as our quiver above, so is there a connection?
A quilt is a gadget to study transitive permutation representations of the braid group $B_3 $ (rather than its quotient, the modular group $PSL_2(\mathbb{Z}) = B_3/\langle Z \rangle $ where $\langle Z \rangle $ is the cyclic center of $B_3 $. The $Z $-stabilizer subgroup of all elements in a transitive permutation representation of $B_3 $ is the same and hence of the form $\langle Z^M \rangle $ where M is called the modulus of the representation. The arrow-data of a quilt, that is the direction of certain edges and their labeling with numbers from $\mathbb{Z}/M \mathbb{Z} $ (which have to satisfy some requirements, the flow rules, but more about that another time) encode the Z-action on the permutation representation. The dimension of the representation is $M \times k $ where $k $ is the number of half-edges in the dessin. In the above example, the modulus is 5 and the dessin has 3 (half)edges, so it depicts a 15-dimensional permutation representation of $B_3 $.
If we forget the Z-action (that is, the arrow information), we get a permutation representation of the modular group (that is a dessin). So, if we delete the labels and directions on the edges we get what Hsu calls a modular quilt, that is, a picture consisting of thick edges (the dessin) together with dotted edges which are called the seams of the modular quilt. The modular quilt is merely another way to depict a fundamental domain of the corresponding subgroup of the modular group. For the above example, we have the indicated correspondences between the fundamental domain of $\Gamma_0(2) $ in the upper half-plane (on the left) and as a modular quilt (on the right)

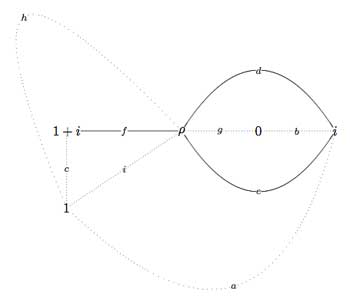
That is, we can also get our quiver (or its opposite quiver) from the modular quilt by fixing the orientation of one 2-cell. For example, if we fix the orientation of the 2-cell $\vec{fch} $ we get our quiver back from the modular quilt

\[
\xymatrix{i \ar[rr]^a \ar[dd]^b & & 1 \ar@/^/[ld]^h \ar@/_/[ld]_i \\
& \rho \ar@/^/[lu]^d \ar@/_/[lu]_e \ar[rd]^f & \\
0 \ar[ru]^g & & i+1 \ar[uu]^c}
\]
This shows that the quiver (or its opposite) associated to a (conjugacy class of a) subgroup of $PSL_2(\mathbb{Z}) $ does not depend on the choice of embedding of the dessin (or associated cuboid tree diagram) in the upper half-plane. For, one can get the modular quilt from the dessin by adding one extra vertex for every connected component of the complement of the dessin (in the example, the two vertices corresponding to 0 and 1) and drawing a triangulation from them (the dotted lines or ‘seams’).
One Comment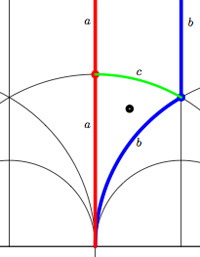 For example, the modular group itself is represented by the Farey symbol
For example, the modular group itself is represented by the Farey symbol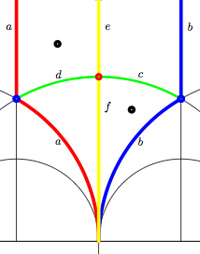 Okay, let’s look at the next case, that of the unique index 2 subgroup $\Gamma_2 $ represented by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] or the dessin (the two green edges) or by its fundamental domain consisting of the 4 triangles where again the left and right vertical boundaries are to be identified in parts.
Okay, let’s look at the next case, that of the unique index 2 subgroup $\Gamma_2 $ represented by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\bullet} & 0 \ar@{-}[r]_{\bullet} & \infty}[/tex] or the dessin (the two green edges) or by its fundamental domain consisting of the 4 triangles where again the left and right vertical boundaries are to be identified in parts.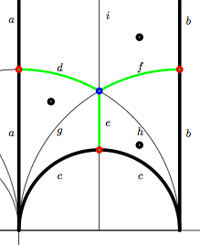 As a mental check, verify that the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] , whose fundamental domain with identifications is given on the left, has as its associated quiver picture
As a mental check, verify that the index 3 subgroup determined by the Farey symbol [tex]\xymatrix{\infty \ar@{-}[r]_{\circ} & 0 \ar@{-}[r]_{\circ} & 1 \ar@{-}[r]_{\circ} & \infty}[/tex] , whose fundamental domain with identifications is given on the left, has as its associated quiver picture
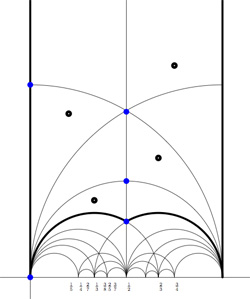 we get the special polygonal region bounded by the thick edges, the vertical edges are identified as are the two bottom edges. Hence, this fundamental domain has 6 vertices (the 5 blue dots and the point at $i \infty $) and 8 hyperbolic triangles (4 colored black, indicated by a black dot, and 4 white ones).
we get the special polygonal region bounded by the thick edges, the vertical edges are identified as are the two bottom edges. Hence, this fundamental domain has 6 vertices (the 5 blue dots and the point at $i \infty $) and 8 hyperbolic triangles (4 colored black, indicated by a black dot, and 4 white ones).