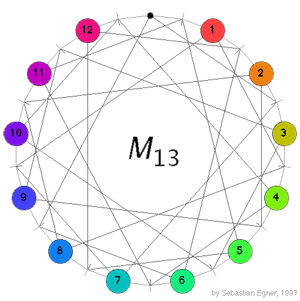
Conway’s puzzle M(13) is a variation on the 15-puzzle played with the 13 points in the projective plane $\mathbb{P}^2(\mathbb{F}_3) $. The desired position is given on the left where all the counters are placed at at the points having that label (the point corresponding to the hole in the drawing has label 0). A typical move consists in choosing a line in the plane going through the point where the hole is, choose one of the three remaining points on this line and interchange the counter on it for the hole while at the same time interchanging the counters on the other two points. In the drawing on the left, lines correspond to the little-strokes on the circle and edges describe which points lie on which lines. For example, if we want to move counter 5 to the hole we notice that both of them lie on the line represented by the stroke just to the right of the hole and this line contains also the two points with counters 1 and 11, so we have to replace these two counters too in making a move. Today we will describe the groupoid corresponding to this slide-puzzle so if you want to read on, it is best to play a bit with Sebastian Egner’s M(13) Java Applet to see the puzzle in action (and to use it to verify the claims made below). Clicking on a counter performs the move taking the counter to the hole.
Tag: puzzle
In the 15-puzzle groupoid 1 we have seen that the legal positions of the classical 15-puzzle are the objects of a category in which every morphism is an isomorphism (a groupoid ). Today, we will show that there are exactly 10461394944000 objects (legal positions) in this groupoid. The crucial fact is that positions with the hole in a fixed place can be identified with the elements of the alternating group $A_{15} $, a fact first proved by William Edward Story in 1879 in a note published in the American Journal of Mathematics.
Recall from last time that the positions reachable from the initial position can be encoded as $\boxed{\tau} $ where $\tau $ is the permutation on 16 elements (the 15 numbered squares and 16 for the hole) such that $\tau(i) $ tells what number in the position lies on square $i $ of the initial position. The set of all reachable positions are the objects of our category. A morphism $\boxed{\tau} \rightarrow \boxed{\sigma} $ is a legal sequence of slide-moves starting from position $\boxed{\tau} $ and ending at position $\boxed{\sigma} $. That is,
$\boxed{\sigma} = (16,i_k)(16,i_{k-1}) \cdots (16,i_2)(16,i_1) \boxed{\tau} $
Leave a CommentBefore we go deeper into Conway’s M(13) puzzle, let us consider a more commonly known sliding puzzle: the 15-puzzle. A heated discussion went on a couple of years ago at sci-physics-research, starting with this message. Lubos Motl argued that group-theory is sufficient to analyze the problem and that there is no reason to resort to groupoids (‘The human(oids) who like groupoids…’ and other goodies, in pre-blog but vintage Motl-speak) whereas ‘Jason’ defended his viewpoint that a groupoid is the natural symmetry for this puzzle.
I’m mostly with Lubos on this. All relevant calculations are done in the symmetric group $S_{16} $ and (easy) grouptheoretic results such as the distinction between even and odd permutations or the generation of the alternating groups really crack the puzzle. At the same time, if one wants to present this example in class, one has to be pretty careful to avoid confusion between permutations encoding positions and those corresponding to slide-moves. In making such a careful analysis, one is bound to come up with a structure which isn’t a group, but is precisely what some people prefer to call a groupoid (if not a 2-group…).
One Comment