Skip to content →

Tag: noncommutative

F_un with Manin

Published September 10, 2008 by lievenlb

Amidst all LHC-noise, Yuri I. Manin arXived today an interesting paper Cyclotomy and analytic geometry over $\mathbb{F}_1 $.

The paper gives a nice survey of the existent literature and focusses on the crucial role of roots of unity in the algebraic geometry over the non-existent field with one element $\mathbb{F}_1 $ (in French called ‘F-un’). I have tried to do a couple of posts on F-un some time ago but now realize, reading Manin’s paper, I may have given up way too soon…

At several places in the paper, Manin hints at a possible noncommutative geometry over $\mathbb{F}_1 $ :

This is the appropriate place to stress that in a wider context of Toen-Vaqui ‘Au-dessous de Spec Z’, or eventually in noncommutative $\mathbb{F}_1 $-geometry, teh spectrum of $\mathbb{F}_1 $ loses its privileged position as a final object of a geometric category. For example, in noncommutative geometry, or in an appropriate category of stacks, the quotient of this spectrum modulo the trivial action of a group must lie below this spectrum.

Soule’s algebras $\mathcal{A}_X $ are a very important element of the structure, in particular, because they form a bridge to Arakelov geometry. Soule uses concrete choices of them in order to produce ‘just right’ supply of morphisms, without a priori constraining these choices formally. In this work, we use these algebras and their version also to pave a way to the analytic (and possibly non-commutative) geometry over $\mathbb{F}_1 $.

Back when I was writing the first batch of F-un posts, I briefly contemplated the possibility of a noncommutative geometry over $\mathbb{F}_1 $, but quickly forgot about it because I thought it would be forced to reduce to commutative geometry.

Here is the quick argument : noncommutative geometry is really the study of coalgebras (see for example my paper or if you prefer more trustworthy sources the Kontsevich-Soibelman paper). Now, unless I made a mistake, I think all coalgebras over $\mathbb{F}_1 $ must be co-commutative (even group-like), so reducing to commutative geometry.

Surely, I’m missing something…

9 Comments

the future of this blog (2)

Published August 14, 2008 by lievenlb

is decided : I’ll keep maintaining this URL until new-year’s eve. At that time I’ll be blogging here for 5 years…

The few encounters I’ve had with architects, taught me this basic lesson of life : the main function of several rooms in a house changes every 5 years (due to children and yourself getting older).

So, from january 1st 2009, I’ll be moving out of here. I will leave the neverendingbooks-site intact for some time to come, so there is no need for you to start archiving it en masse, yet.

Previously I promised to reconsider this blog’s future over a short vacation, but as vacation is looking to be as illusory as the 24-dimensional monster-manifold, I spend my time throwing up ideas into thin and, it seems, extremely virtual air.

Some of you will think this is a gimmick, aiming to attract more comments (there is no post getting more responses than an imminent-end-to-this-blog-post) but then I hope to have settled this already. Neverendingbooks will die on 31st of december 2008. The only remaining issue being : do I keep on blogging or do I look for another time-consumer such as growing tomatoes or, more probably, collecting single malts…

For reasons I’ve stated before, I can see little future in anything but a conceptual-, group- blog. The first part I can deal with, but for the second I’ll be relying on others. So, all I can do is offer formats hoping that some of you are willing to take the jump and try it out together.

Such as in the bloomsday-post where I sketched the BistroMath blog-concept. Perhaps you thought I was just kidding, hoping for people to commit themselves and them calling “Gotcha…”. Believe me, 30 years of doing mathematics have hardwired my brains such that I always genuinely believe in the things I write down at the moment I do (but equally, if someone offers me enough evidence to the contrary, I’ll drop any idea on the spot).

I still think the BistroMath-project has the potential of leading to a bestseller but Ive stated I was not going to pursue the idea if not at least 5 people were willing to join and at least 1 publisher showed an interest. Ironically, I got 2 publishers interested but NO contributors… End of that idea.

Today I offer another conceptual group-blog : the Noether-boys seminar (with tagline ; _the noncommutative experts’ view on 21st century mathematics_). And to make it a bit more concrete Ive even designed a potential home-page :



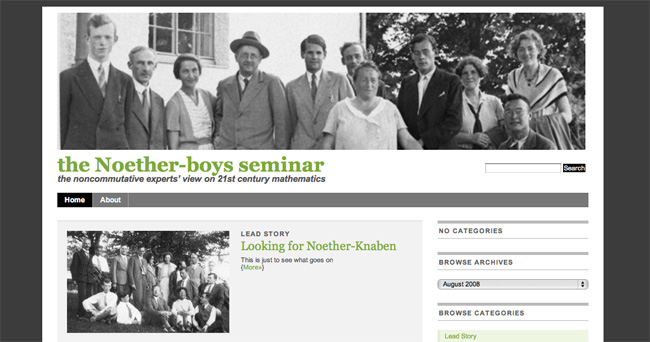
So, what’s the deal? In the 1930-ties Emmy Noether collected around her in Goettingen an exceptionally strong group of students and collaborators (among them : Deuring, Fitting, Levitski, Schilling, Tsen, Weber, Witt, VanderWaerden, Brauer, Artin, Hasse, MacLane, Bernays, Tausky, Alexandrov… to name a few).

Collectively, they were know as the “Noether-boys” (or “Noether-Knaben” or “Trabanten” in German) and combined seminar with a hike to the nearby hills or late-night-overs at Emmy’s apartment. (Btw. there’s nothing sexist about Noether-boys. When she had to leave Germany for Bryn Mawr College, she replaced her boys to form a group of Noether-girls, and even in Goettingen there were several women in the crowd).

They were the first generation of mathematicians going noncommutative and had to struggle a bit to get their ideas accepted.
I’d like to know what they might think about the current state of mathematics in which noncommutativity seems to be generally accepted, even demanded if you want to act fashionable.

I’m certain half of the time they would curse intensely, and utter something like ‘steht shon alles bei Frau Noether…’ (as Witt is witnessed to have done at least once), and about half the time they might get genuinely interested, and be willing to try and explain the events leading up to this to their fellow “Trabanten”. Either way, it would provide excellent blog-posts.

So I’m looking for people willing to borrow the identity of one of the Noether-boys or -girls. That is, you have to be somewhat related to their research and history to offer a plausible reaction to recent results in either noncommutative algebra, noncommutative geometry or physics. Assuming their identity you will then blog to express your (that is, ‘their’) opinion and interact with your fellow Trabanten as might have been the case in the old days…

I’d like to keep Emmy Noether for the admin-role of the blog but all other characters are free at this moment (except I’m hoping that no-one will choose my favourite role, which is probably the least expected of them anyway).

So please, if you think this concept might lead to interesting blogging, contact me! If I don’t get any positives in this case either, I might think about yet another concept (or instead may give up entirely).

4 Comments

the future of this blog

Published August 6, 2008 by lievenlb

Some weeks ago Peter Woit of Not Even Wrong and Bee of Backreaction had a video-chat on all sorts of things (see the links above to see the whole clip) including the nine minute passage below on ‘the future of (science) blogs’.

click here to see the video

The crucial point being that blogging takes time and that one often feels that the time invested might have been better spend doing other things. Bee claims it doesn’t take her that long to write a post, but given their quality, I would be surprised if it took her less than one to two hours on average.

Speaking for myself, I’ve uploaded two (admittedly short) notes to the arXiv recently. The shorter one took me less time than an average blogpost, the longer one took me about the time I need for one of the better posts. So, is it really justified to invest that amount of time in something as virtual as a blog?

Probably it all depends on the type of blog you’re running and what goal (if any) you want to achieve with it.

I can see the point in setting up a blog connected to a book you once wrote or intend to write (such as Not Even Wrong or Terry Tao).

I can also understand that people start a blog to promote their research-topic or to have a social function for people interested in the same topic (such as Noncommutative Geometry or the n-category cafe).

I can even imagine the energy boost resulting from setting up a group-blog with fellow researchers working at the same place (such as Secret Blogging Seminar or the Everything Seminar and some others).

So, there are plenty of good reasons to start and keep investing in a serious mathematical blog (as opposed to mere link-blogs (I won’t mention examples) or standard-textbook-excerpts-blogs (again, I’ll refrain from giving examples)).

What is needed is either a topical focus or a clear medium term objective. Unfortunately, this blog has neither…

At present, I feel like the journalist, spending too much time getting into a subject merely to write a short piece on it for today’s paper, which will be largely forgotten by tomorrow, but still hoping that his better writings will result into something having a longer half-life…

That is, I need to reconsider the future of this blog and will do so over a short vacation. As always, suggestions you might have are welcome. Perhaps I should take the bait offered by John McKay in his comment yesterday and do a series on the illusory 24-dimensional monster-manifold.

At the very least it would take this blog back to the only time when it was somewhat focussed on a single topic and was briefly called MoonshineMath. But then, even this is not without risks…



7 Comments