Some weeks ago Peter Woit of Not Even Wrong and Bee of Backreaction had a video-chat on all sorts of things (see the links above to see the whole clip) including the nine minute passage below on ‘the future of (science) blogs’.
The crucial point being that blogging takes time and that one often feels that the time invested might have been better spend doing other things. Bee claims it doesn’t take her that long to write a post, but given their quality, I would be surprised if it took her less than one to two hours on average.
Speaking for myself, I’ve uploaded two (admittedly short) notes to the arXiv recently. The shorter one took me less time than an average blogpost, the longer one took me about the time I need for one of the better posts. So, is it really justified to invest that amount of time in something as virtual as a blog?
Probably it all depends on the type of blog you’re running and what goal (if any) you want to achieve with it.
I can see the point in setting up a blog connected to a book you once wrote or intend to write (such as Not Even Wrong or Terry Tao).
I can also understand that people start a blog to promote their research-topic or to have a social function for people interested in the same topic (such as Noncommutative Geometry or the n-category cafe).
I can even imagine the energy boost resulting from setting up a group-blog with fellow researchers working at the same place (such as Secret Blogging Seminar or the Everything Seminar and some others).
So, there are plenty of good reasons to start and keep investing in a serious mathematical blog (as opposed to mere link-blogs (I won’t mention examples) or standard-textbook-excerpts-blogs (again, I’ll refrain from giving examples)).
What is needed is either a topical focus or a clear medium term objective. Unfortunately, this blog has neither…
At present, I feel like the journalist, spending too much time getting into a subject merely to write a short piece on it for today’s paper, which will be largely forgotten by tomorrow, but still hoping that his better writings will result into something having a longer half-life…
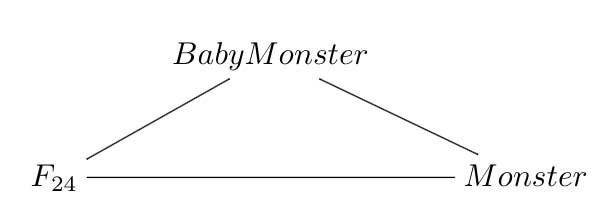
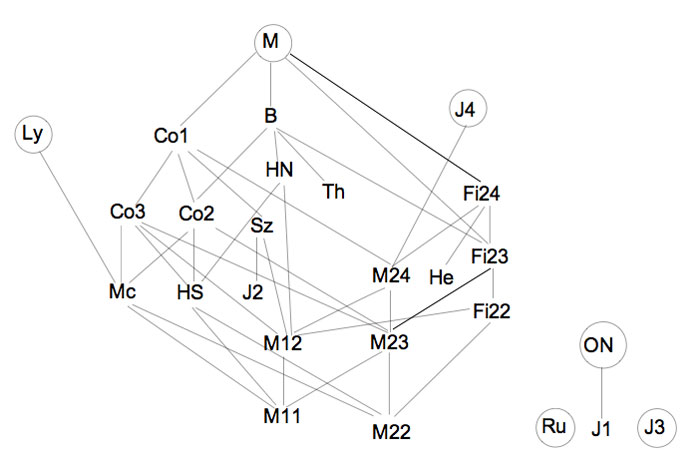
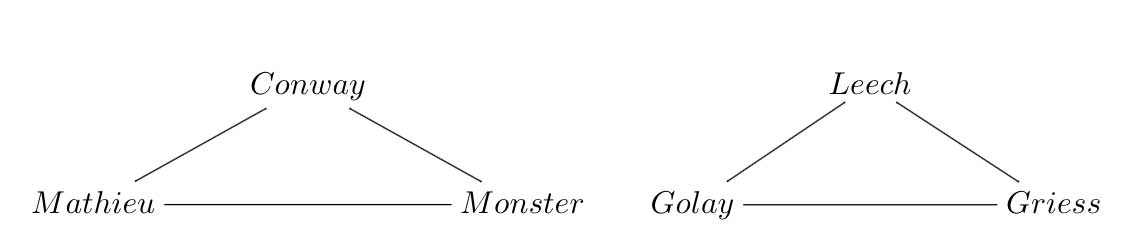
That is, I need to reconsider the future of this blog and will do so over a short vacation. As always, suggestions you might have are welcome. Perhaps I should take the bait offered by John McKay in his comment yesterday and do a series on the illusory 24-dimensional monster-manifold.
At the very least it would take this blog back to the only time when it was somewhat focussed on a single topic and was briefly called MoonshineMath. But then, even this is not without risks…