Skip to content →

Tag: moonshine

capita selecta

Published April 22, 2004 by lievenlb


Rather than going to the NOG
III Workshop I think it is more fun to give a talk for the Capita
Selecta-course for 2nd year students on “Monstrous Moonshine”. If
I manage to explain to them at least something, I think I am in good
shape for next year\’s Baby Geometry (first year) course. Besides,
afterwards I may decide to give some details of Borcherds\’ solution next year in my 3rd year
Geometry-course…(but this may just be a little bit
over-optimistic).
Anyway, this is what I plan to do in my
lecture : explain both sides of the McKay-observation
that

196 884 = 196 883 + 1

that is, I\’ll give
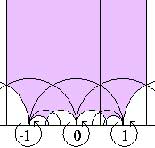
the action of the modular group on the upper-half plane and prove that
its fundamental domain is just C using the modular j-function (left hand
side) and sketch the importance of the Monster group and its
representation theory (right hand side). Then I\’ll mention Ogg\’s
observation that the only subgroups Gamma(0,p)+ of SL(2,Z)
for which the fundamental domain has genus zero are the prime divisors
p of teh order of the Monster and I\’ll come to moonshine
conjecture of Conway and Norton (for those students who did hear my talk
on Antwerp sprouts, yes both Conway and Simon Norton (via his
SNORT-go) did appear there too…) and if time allows it, I\’ll sketch
the main idea of the proof. Fortunately, Richard Borcherds has written
some excellent expository papers I can use (see his papers-page and I also discovered a beautiful
moonshine-page by Helena Verrill which will make my job a lot
easier.
Btw. yesterday\’s Monster was taken from her other monster story…

Leave a Comment

25 years monstrous moonshine

Published April 21, 2004 by lievenlb

Writing a survey paper is a highly underestimated task. I once
tried it out with \’Centers of generic division algebras : the
rationality problem 1965-1990\’ and it took me a lot of time and that
was on a topic with only 10 to 15 key papers to consider… The task of
writing a survey paper on a topic with any breadth must be much more
difficult. Last week, Terry Gannon posted a survey paper on the arXiv :
Monstrous Moonshine : The first twenty-five years
which gives a very readable introduction to this exciting topic. It has
a marvelous opening line :

It has been approximately
twenty-five years since John McKay remarked that

196 884 = 196 883 +
 1

Anyone who is puzzled by this line (“So what?”)
should definitely have a go at this paper! Still not convinced? Here is
the second sentence :

That time has seen the discovery of
important structures, the establishment of another deep connection
between number theory and algebra, and a reinforcement of a new era of
cooperation between pure mathematics and mathematical
physics.

For the remaining sentences (quite a few, the paper
is 33 pages long) I happily refer you to the paper.

Leave a Comment

Borcherds’ monster papers

Published March 27, 2004 by lievenlb


Yesterday morning I thought that I could use some discussions I had a
week before with Markus Reineke to begin to make sense of one
sentence in Kontsevich’ Arbeitstagung talk Non-commutative smooth
spaces :

It seems plausible that Borcherds’ infinite rank
algebras with Monstrous symmetry can be realized inside Hall-Ringel
algebras for some small smooth noncommutative
spaces

However, as I’m running on a 68K RAM-memory, I
didn’t recall the fine details of all connections between the monster,
moonshine, vertex algebras and the like. Fortunately, there is the vast
amount of knowledge buried in the arXiv and a quick search on Borcherds gave me a
list of 17 papers. Among
these there are some delightful short (3 to 8 pages) expository papers
that gave me a quick recap on things I once must have read but forgot.
Moreover, Richard Borcherds has the gift of writing at the same time
readable and informative papers. If you want to get to the essence of
things in 15 minutes I can recommend What
is a vertex algebra? (“The answer to the question in the title is
that a vertex algebra is really a sort of commutative ring.”), What
is moonshine? (“At the time he discovered these relations, several
people thought it so unlikely that there could be a relation between the
monster and the elliptic modular function that they politely told McKay
that he was talking nonsense.”) and What
is the monster? (“3. It is the automorphism group of the monster
vertex algebra. (This is probably the best answer.)”). Borcherds
maintains also his homepage on which I found a few more (longer)
expository papers : Problems in moonshine and Automorphic forms and Lie algebras. After these
preliminaries it was time for the real goodies such as The
fake monster formal group, Quantum vertex algebras and the like.
After a day of enjoyable reading I think I’m again ‘a point’
wrt. vertex algebras. Unfortunately, I completely forgot what all this
could have to do with Kontsevich’ remark…

Leave a Comment