Tag: modular

Before the vacation I finished a rewrite of the One quiver to rule them
all note. The main point of that note was to associate to any qurve
$A$ (formerly known as a quasi-free algebra in the terminology of
Cuntz-Quillen or a formally smooth algebra in the terminology of
Kontsevich-Rosenberg) a quiver $Q(A)$ and a dimension vector $\alpha_A$
such that $A$ is etale isomorphic (in a yet to be defined
non-commutative etale toplogy) to a ring Morita equivalent to the path
algebra $lQ(A)$ where the Morita setting is determined by the dimension
vector $\alpha_A$. These “one-quiver settings” are easy to
work out for a group algebra $lG$ if $G$ is the amalgamated free product
of finite groups $G = H_1 \bigstar_H H_2$.

Here is how to do
this : construct a bipartite quiver with the left vertices corresponding
to the irreducible representations of $H_1$, say ${ S_1, .. ,S_k }$ of
dimensions $(d_1, .. ,d_k)$ and the right vertices corresponding to the
irreducible representations of $H_2$, ${ T_1, .. ,T_l }$ of dimensions
$(e_1, .. ,e_l)$. The number of arrows from the $i$-th left vertex to
the $j$-th right vertex is given by the dimension of $Hom_H(S_i,T_j)$
This is the quiver I call the Zariski quiver for $G$ as the finite
dimensional $G$-representations correspond to $\theta$-semistable
representations of this quiver for the stability structure $\theta=(d_1, .. ,d_k ; -e_1, .. ,-e_l)$. The one-quiver $Q(G)$ has vertices
corresponding to the minimal $\theta$-stable dimension vectors (say
$\alpha,\beta, ..$of the Zariski quiver and with the number of arrows
between two such vertices determined by $\delta_{\alpha \beta}-\chi(\alpha,\beta)$ where $\chi$ is the Euler form of the Zariski
quiver. In the old note I've included the example of the projective
modular group $PSL_2(Z) = Z_2 \bigstar Z_3$ (which can easily be
generalized to the modular group $SL_2(Z) = Z_4 \bigstar_{Z_2} Z_6$)
which turns out to be the double of the extended Dynkin quiver
$\tilde{A_5}$. In the rewrite I've also included an example of a
congruence subgroup $\Gamma_0(2) = Z_4 \bigstar_{Z_2}^{HNN}$ which is an
HNN-extension. These are somehow the classical examples of interesting
amalgamated (HNN) groups and one would like to have plenty of other
interesting examples. Yesterday I read a paper by Karen Vogtmann called

Automorphisms of free groups and outer space in which I encountered
an amalgamated product decomposition for $GL_2(Z) = D_8 \bigstar_{Z_2 \times Z_2} (S_3 \times Z_2)$where $D_8$ is the diheder group of 8
elements. When I got back from vacation I found a reference to this
result in my mail-box from Warren Dicks. Theorem 23.1, p. 82, in Heiner
Zieschang, Finite Groups of Mapping Classes of Surfaces, LNM 875,
Springer, Berlin, 1981.

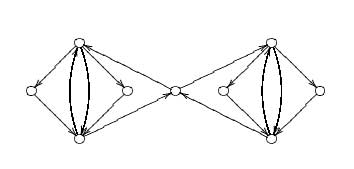
I worked out the one-quiver and it has
the somewhat strange form depicted above. It is perfectly possible that
I made mistakes so if you find another result, please let me know.

added material (febr 2007) : mistakes were made and
the correct one quiver can be found elsewhere on this blog.