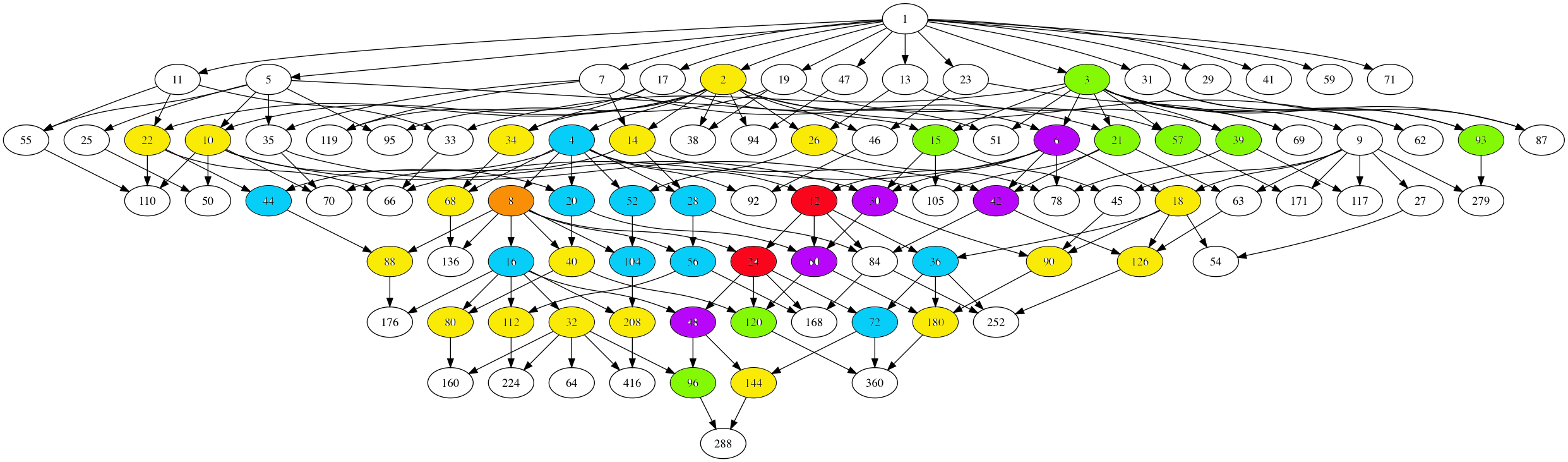
Time to wrap up my calculations on the moonshine picture, which is the subgraph of Conway’s Big Picture needed to describe all 171 moonshine groups.
No doubt I’ve made mistakes. All corrections are welcome. The starting point is the list of 171 moonshine groups which are in the original Monstrous Moonshine paper.
The backbone is given by the $97$ number lattices, which are closed under taking divisors and were found by looking at all divisors of the numbers $N=n \times h$ for the 171 moonshine groups of the form $N+e,f,\dots$ or $(n|h)+e,f,\dots$.
The Hasse-diagram of this poset (under division) is here (click on the image to get a larger version)
There are seven types of coloured numbers, each corresponding to number-lattices which have the same local structure in the moonshine picture, as in the previous post.
The white numbered lattices have no further edges in the picture.
The yellow number lattices (2,10,14,18,22,26,32,34,40,68,80,88,90,112,126,144,180,208 = 2M) have local structure
\[
\xymatrix{& \color{yellow}{2M} \ar@{-}[r] & M \frac{1}{2}} \]
The green number lattices (3,15,21,39,57,93,96,120 = 3M) have local structure
\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[r] & \color{green}{3M} \ar@[red]@{-}[r] & M \frac{2}{3}} \]
The blue number lattices (4,16,20,28,36,44,52,56,72,104 = 4M) have as local structure
\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{blue}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
& & M \frac{3}{4}} \]
where the leftmost part is redundant as they are already included in the yellow-bit.
The purple number lattices (6,30,42,48,60 = 6M) have local structure
\[
\xymatrix{M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{purple}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]
where again the lefmost part is redundant, and I forgot to add the central part in the previous post… (updated now).
The unique brown number lattice 8 has local structure
\[
\xymatrix{& & 1 \frac{1}{4} \ar@{-}[d] & & 1 \frac{1}{8} \ar@{-}[d] & \\
& 1 \frac{1}{2} \ar@{-}[d] & 2 \frac{1}{2} \ar@{-}[r] \ar@{-}[d] & 1 \frac{3}{4} & 2 \frac{1}{4} \ar@{-}[r] & 1 \frac{5}{8} \\
1 \ar@{-}[r] & 2 \ar@{-}[r] & 4 \ar@{-}[r] & \color{brown}{8} \ar@{-}[r] & 4 \frac{1}{2} \ar@{-}[d] \ar@{-}[u] & \\
& & & 1 \frac{7}{8} \ar@{-}[r] & 2 \frac{3}{4} \ar@{-}[r] & 1 \frac{3}{8}} \]
The local structure in the two central red number lattices (not surprisingly 12 and 24) looks like the image in the previous post, but I have to add some ‘forgotten’ lattices.
That’ll have to wait…
Leave a Comment