I’m trying to get into the latest Manin-Marcolli paper Quantum Statistical Mechanics of the Absolute Galois Group on how to create from Grothendieck’s dessins d’enfant a quantum system, generalising the Bost-Connes system to the non-Abelian part of the absolute Galois group $Gal(\overline{\mathbb{Q}}/\mathbb{Q})$.
In doing so they want to extend the action of the multiplicative monoid $\mathbb{N}_{\times}$ by power maps on the roots of unity to the action of a larger monoid on all dessins d’enfants.
Here they use an idea, originally due to Jordan Ellenberg, worked out by Melanie Wood in her paper Belyi-extending maps and the Galois action on dessins d’enfants.

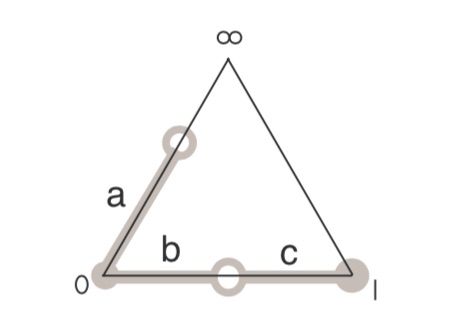
To grasp this, it’s best to remember what dessins have to do with Belyi maps, which are maps defined over $\overline{\mathbb{Q}}$
\[
\pi : \Sigma \rightarrow \mathbb{P}^1 \]
from a Riemann surface $\Sigma$ to the complex projective line (aka the 2-sphere), ramified only in $0,1$ and $\infty$. The dessin determining $\pi$ is the 2-coloured graph on the surface $\Sigma$ with as black vertices the pre-images of $0$, white vertices the pre-images of $1$ and these vertices are joined by the lifts of the closed interval $[0,1]$, so the number of edges is equal to the degree $d$ of the map.
Wood considers a very special subclass of these maps, which she calls Belyi-extender maps, of the form
\[
\gamma : \mathbb{P}^1 \rightarrow \mathbb{P}^1 \]
defined over $\mathbb{Q}$ with the additional property that $\gamma$ maps $\{ 0,1,\infty \}$ into $\{ 0,1,\infty \}$.
The upshot being that post-compositions of Belyi’s with Belyi-extenders $\gamma \circ \pi$ are again Belyi maps, and if two Belyi’s $\pi$ and $\pi’$ lie in the same Galois orbit, then so must all $\gamma \circ \pi$ and $\gamma \circ \pi’$.
The crucial Ellenberg-Wood idea is then to construct “new Galois invariants” of dessins by checking existing and easily computable Galois invariants on the dessins of the Belyi’s $\gamma \circ \pi$.
For this we need to know how to draw the dessin of $\gamma \circ \pi$ on $\Sigma$ if we know the dessins of $\pi$ and of the Belyi-extender $\gamma$. Here’s the procedure

Here, the middle dessin is that of the Belyi-extender $\gamma$ (which in this case is the power map $t \rightarrow t^4$) and the upper graph is the unmarked dessin of $\pi$.
One has to replace each of the black-white edges in the dessin of $\pi$ by the dessin of the expander $\gamma$, but one must be very careful in respecting the orientations on the two dessins. In the upper picture just one edge is replaced and one has to do this for all edges in a compatible manner.
Thus, a Belyi-expander $\gamma$ inflates the dessin $\pi$ with factor the degree of $\gamma$. For this reason i prefer to call them dessinflateurs, a contraction of dessin+inflator.
In her paper, Melanie Wood says she can separate dessins for which all known Galois invariants were the same, such as these two dessins,
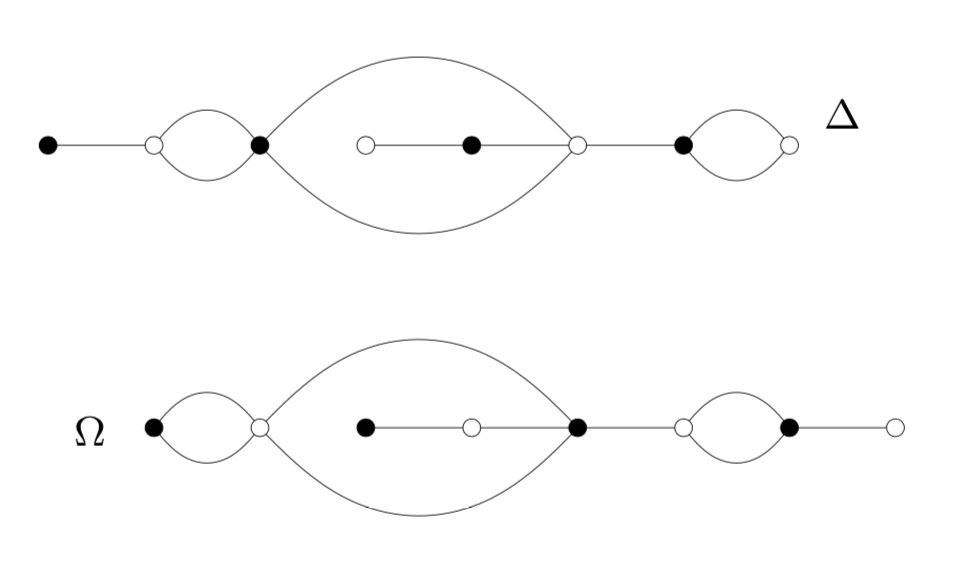
by inflating them with a suitable Belyi-extender and computing the monodromy group of the inflated dessin.
This monodromy group is the permutation group generated by two elements, the first one gives the permutation on the edges given by walking counter-clockwise around all black vertices, the second by walking around all white vertices.
For example, by labelling the edges of $\Delta$, its monodromy is generated by the permutations $(2,3,5,4)(1,6)(8,10,9)$ and $(1,3,2)(4,7,5,8)(9,10)$ and GAP tells us that the order of this group is $1814400$. For $\Omega$ the generating permutations are $(1,2)(3,6,4,7)(8,9,10)$ and $(1,2,4,3)(5,6)(7,9,8)$, giving an isomorphic group.
Let’s inflate these dessins using the Belyi-extender $\gamma(t) = -\frac{27}{4}(t^3-t^2)$ with corresponding dessin
It took me a couple of attempts before I got the inflated dessins correct (as i knew from Wood that this simple extender would not separate the dessins). Inflated $\Omega$ on top:

Both dessins give a monodromy group of order $35838544379904000000$.
Now we’re ready to do serious work.
Melanie Wood uses in her paper the extender $\zeta(t)=\frac{27 t^2(t-1)^2}{4(t^2-t+1)^3}$ with associated dessin

and says she can now separate the inflated dessins by the order of their monodromy groups. She gets for the inflated $\Delta$ the order $19752284160000$ and for inflated $\Omega$ the order $214066877211724763979841536000000000000$.
It’s very easy to make mistakes in these computations, so probably I did something horribly wrong but I get for both $\Delta$ and $\Omega$ that the order of the monodromy group of the inflated dessin is $214066877211724763979841536000000000000$.
I’d be very happy when someone would be able to spot the error!


