John Farey (1766-1826) was a geologist of sorts. Eyles, quoted on the math-biographies site described his geological work as
“As a geologist Farey is entitled to respect for the work which he carried out himself, although it has scarcely been noticed in the standard histories of geology.”
That we still remember his name after 200 years is due to a short letter he wrote in 1816 to the editor of the Philosophical Magazine
“On a curious Property of vulgar Fractions.
By Mr. J. Farey, Sen. To Mr. Tilloch
Sir. – On examining lately, some very curious and elaborate Tables of “Complete decimal Quotients,” calculated by Henry Goodwyn, Esq. of Blackheath, of which he has printed a copious specimen, for private circulation among curious and practical calculators, preparatory to the printing of the whole of these useful Tables, if sufficient encouragement, either public or individual, should appear to warrant such a step: I was fortunate while so doing, to deduce from them the following general property; viz.
If all the possible vulgar fractions of different values, whose greatest denominator (when in their lowest terms) does not exceed any given number, be arranged in the order of their values, or quotients; then if both the numerator and the denominator of any fraction therein, be added to the numerator and the denominator, respectively, of the fraction next but one to it (on either side), the sums will give the fraction next to it; although, perhaps, not in its lowest terms.
For example, if 5 be the greatest denominator given; then are all the possible fractions, when arranged, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, and 4/5; taking 1/3, as the given fraction, we have (1+1)/(5+3) = 2/8 = 1/4 the next smaller fraction than 1/3; or (1+1)/(3+2) = 2/5, the next larger fraction to 1/3. Again, if 99 be the largest denominator, then, in a part of the arranged Table, we should have 15/52, 28/97, 13/45, 24/83, 11/38, &c.; and if the third of these fractions be given, we have (15+13)/(52+45) = 28/97 the second: or (13+11)/(45+38) = 24/83 the fourth of them: and so in all the other cases.
I am not acquainted, whether this curious property of vulgar fractions has been before pointed out?; or whether it may admit of any easy or general demonstration?; which are points on which I should be glad to learn the sentiments of some of your mathematical readers; and am
Sir, Your obedient humble servant,
J. Farey. Howland-street.”
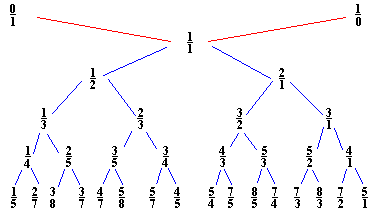
So, if we interpolate “childish addition of fractions” $\frac{a}{b} \oplus \frac{c}{d} = \frac{a+c}{b+d} $ and start with the numbers $0 = \frac{0}{1} $ and $\infty = \frac{1}{0} $ we get the binary Farey-tree above. For a fixed natural number n, if we stop the interpolation whenever the denominator of the fraction would become larger than n and order the obtained fractions (smaller or equal to one) we get the Farey sequence F(n). For example, if n=3 we start with the sequence $ \frac{0}{1},\frac{1}{1} $. The next step we get $\frac{0}{1},\frac{1}{2},\frac{1}{1} $ and the next step gives
$\frac{0}{1},\frac{1}{3},\frac{1}{2},\frac{2}{3},\frac{1}{1} $
and as all the denomnators of childish addition on two consecutive fractions will be larger than 3, the above sequence is F(3). A remarkable feature of the series F(n) is that if $\frac{a}{b} $ and $\frac{c}{d} $ are consecutive terms in F(n), then
$det \begin{bmatrix} a & c \\\ b & d \end{bmatrix} = -1 $
and so these two fractions are the endpoints of an even geodesic in the Dedekind tessellation.
A generalized Farey series is an ordered collection of fractions $\infty,x_0,x_1,\cdots,x_n,\infty $ such that $x_0 $ and $x_n $ are integers and some $x_i=0 $. Moreover, writing $x_i = \frac{a_i}{b_i} $ we have that
$det \begin{bmatrix} a_i & a_{i+1} \\\ b_i & b_{i+1} \end{bmatrix} = -1 $
A Farey code is a generalized Farey sequence consisting of all the vertices of a special polygon that lie in $\mathbb{R} \cup \{ \infty \} $ together with side-pairing information. If two consecutive terms are such that the complete geodesic between $x_i $ and $x_{i+1} $ consists of two sides of the polygon which are paired we denote this fact by
[tex]\xymatrix{x_i \ar@{-}[r]_{\circ} & x_{i+1}}[/tex]. If they are the endpoints of two odd sides of the polygon which are paired we denote this by [tex]\xymatrix{x_i \ar@{-}[r]_{\bullet} & x_{i+1}}[/tex]. Finally, if they are the endpoints of a free side which is paired to another free side determined by $x_j $ and $x_{j+1} $ we denote this fact by marking both edges [tex]\xymatrix{x_i \ar@{-}[r]_{k} & x_{i+1}}[/tex] and [tex]\xymatrix{x_j \ar@{-}[r]_{k} & x_{j+1}}[/tex] with the same number.
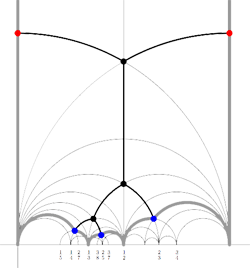
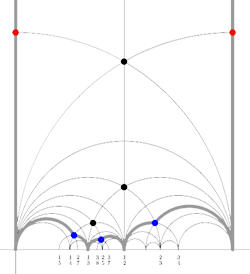
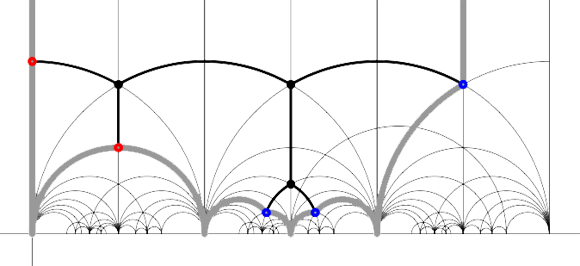
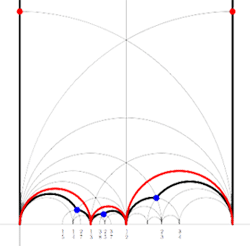For example, for the M(12) special polygon on the left (bounded by the thick black geodesics), the only vertices in $\mathbb{R} \cup \{ \infty \} $ are $\infty,0,\frac{1}{3},\frac{1}{2},1 $. The two vertical lines are free sides and are paired, whereas all other sides of the polygon are odd. Therefore the Farey-code for this Mathieu polygon is
[tex]\xymatrix{\infty \ar@{-}[r]_{1} & 0 \ar@{-}[r]_{\bullet} & \frac{1}{3} \ar@{-}[r]_{\bullet} & \frac{1}{2} \ar@{-}[r]_{\bullet} & 1 \ar@{-}[r]_{1} & \infty}[/tex]
Conversely, to a Farey-code we can associate a special polygon by first taking the hyperbolic convex hull of all the terms in the sequence (the region bounded by the vertical lines and the bottom red circles in the picture on the left) and adding to it for each odd interval [tex]\xymatrix{x_i \ar@{-}[r]_{\bullet} & x_{i+1}}[/tex] the triangle just outside the convex hull consisting of two odd edges in the Dedekind tessellation (then we obtain the region bounded by the black geodesics). Again, the side-pairing of the obained special polygon can be obtained from that of the Farey-code.
This correspondence gives a natural one-to-one correspondence special polygons <---> Farey-codes . _Later_ we will see how the Farey-code determines the group structure of the corresponding finite index subgroup of the modular group $\Gamma = PSL_2(\mathbb{Z}) $.
Reference
Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math 113 (1991) 1053-1133
4 Comments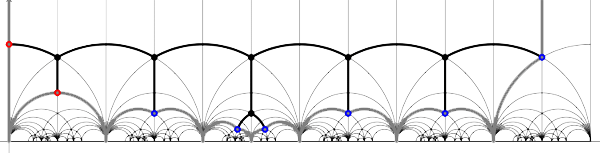
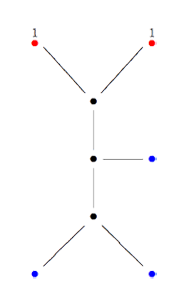
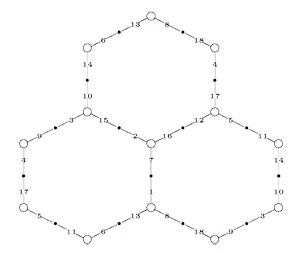
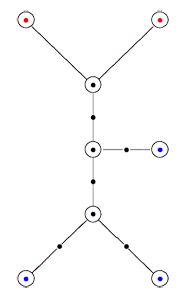Recall that a cuboid tree diagram is a tree such that all internal vertices are 3-valent and have a specified ordering on the incident edges (given by walking counterclockwise around the vertex) and such that all leaf-vertices are tinted blue or red, the latter ones are paired via an involution (indicated by giving paired red vertices the same label). Introduce a new 2-valent vertex on all edges joining two internal vertices or a blue vertex to an internal vertex. So, the picture on the right corresponds to the tree diagram on the left. 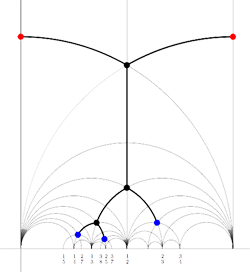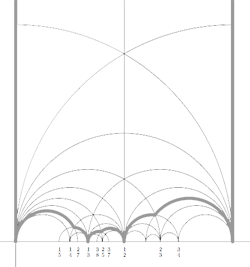Equip this extended tree with a metric such that every edge has length equal to an f-edge in the 
Conjugacy classes of finite index subgroups of the