In ONAG, John Conway proves that the symmetric version of his recursive definition of addition and multiplcation on the surreal numbers make the class On of all Cantor’s ordinal numbers into an algebraically closed Field of characteristic two : On2 (pronounced ‘Onto’), and, in particular, he identifies a subfield
with the algebraic closure of the field of two elements. What makes all of this somewhat confusing is that Cantor had already defined a (badly behaving) addition, multiplication and exponentiation on ordinal numbers.
Over the last week I’ve been playing a bit with sage to prove a few exotic identities involving ordinal numbers. Here’s one of them ($\omega $ is the first infinite ordinal number, that is, $\omega={ 0,1,2,\ldots } $),
$~(\omega^{\omega^{13}})^{47} = \omega^{\omega^7} + 1 $
answering a question in Hendrik Lenstra’s paper Nim multiplication.
However, it will take us a couple of posts before we get there. Let’s begin by trying to explain what brought this on. On september 24th 2008 there was a meeting, intended for a general public, called a la rencontre des dechiffeurs, celebrating the 50th birthday of the IHES.
One of the speakers was Alain Connes and the official title of his talk was “L’ange de la géométrie, le diable de l’algèbre et le corps à un élément” (the angel of geometry, the devil of algebra and the field with one element). Instead, he talked about a seemingly trivial problem : what is the algebraic closure of $\mathbb{F}_2 $, the field with two elements? My only information about the actual content of the talk comes from the following YouTube-blurb
Alain argues that we do not have a satisfactory description of $\overline{\mathbb{F}}_2 $, the algebraic closure of $\mathbb{F}_2 $. Naturally, it is the union (or rather, limit) of all finite fields $\mathbb{F}_{2^n} $, but, there are too many non-canonical choices to make here.
Recall that $\mathbb{F}_{2^k} $ is a subfield of $\mathbb{F}_{2^l} $ if and only if $k $ is a divisor of $l $ and so we would have to take the direct limit over the integers with respect to the divisibility relation… Of course, we can replace this by an increasing sequence of a selection of cofinal fields such as
$\mathbb{F}_{2^{1!}} \subset \mathbb{F}_{2^{2!}} \subset \mathbb{F}_{2^{3!}} \subset \ldots $
But then, there are several such suitable sequences! Another ambiguity comes from the description of $\mathbb{F}_{2^n} $. Clearly it is of the form $\mathbb{F}_2[x]/(f(x)) $ where $f(x) $ is a monic irreducible polynomial of degree $n $, but again, there are several such polynomials. An attempt to make a canonical choice of polynomial is to take the ‘first’ suitable one with respect to some natural ordering on the polynomials. This leads to the so called Conway polynomials.
Conway polynomials for the prime $2 $ have only been determined up to degree 400-something, so in the increasing sequence above we would already be stuck at the sixth term $\mathbb{F}_{2^{6!}} $…
So, what Alain Connes sets as a problem is to find another, more canonical, description of $\overline{\mathbb{F}}_2 $. The problem is not without real-life interest as most finite fields appearing in cryptography or coding theory are subfields of $\overline{\mathbb{F}}_2 $.
(My guess is that Alain originally wanted to talk about the action of the Galois group on the roots of unity, which would be the corresponding problem over the field with one element and would explain the title of the talk, but decided against it. If anyone knows what ‘coupling-problem’ he is referring to, please drop a comment.)
 Surely, Connes is aware of the fact that there exists a nice canonical recursive construction of $\overline{\mathbb{F}}_2 $ due to John Conway, using Georg Cantor’s ordinal numbers.
Surely, Connes is aware of the fact that there exists a nice canonical recursive construction of $\overline{\mathbb{F}}_2 $ due to John Conway, using Georg Cantor’s ordinal numbers.
In fact, in chapter 6 of his book On Numbers And Games, John Conway proves that the symmetric version of his recursive definition of addition and multiplcation on the surreal numbers make the class $\mathbf{On} $ of all Cantor’s ordinal numbers into an algebraically closed Field of characteristic two : $\mathbf{On}_2 $ (pronounced ‘Onto’), and, in particular, he identifies a subfield
$\overline{\mathbb{F}}_2 \simeq [ \omega^{\omega^{\omega}} ] $
with the algebraic closure of $\mathbb{F}_2 $. What makes all of this somewhat confusing is that Cantor had already defined a (badly behaving) addition, multiplication and exponentiation on ordinal numbers. To distinguish between the Cantor/Conway arithmetics, Conway (and later Lenstra) adopt the convention that any expression between square brackets refers to Cantor-arithmetic and un-squared ones to Conway’s. So, in the description of the algebraic closure just given $[ \omega^{\omega^{\omega}} ] $ is the ordinal defined by Cantor-exponentiation, whereas the exotic identity we started out with refers to Conway’s arithmetic on ordinal numbers.
Let’s recall briefly Cantor’s ordinal arithmetic. An ordinal number $\alpha $ is the order-type of a totally ordered set, that is, if there is an order preserving bijection between two totally ordered sets then they have the same ordinal number (or you might view $\alpha $ itself as a totally ordered set, namely the set of all strictly smaller ordinal numbers, so e.g. $0= \emptyset,1= { 0 },2={ 0,1 },\ldots $).
For two ordinals $\alpha $ and $\beta $, the addition $[\alpha + \beta ] $ is the order-type of the totally ordered set $\alpha \sqcup \beta $ (the disjoint union) ordered compatible with the total orders in $\alpha $ and $\beta $ and such that every element of $\beta $ is strictly greater than any element from $\alpha $. Observe that this definition depends on the order of the two factors. For example,$ [1 + \omega] = \omega $ as there is an order preserving bijection ${ \tilde{0},0,1,2,\ldots } \rightarrow { 0,1,2,3,\ldots } $ by $\tilde{0} \mapsto 0,n \mapsto n+1 $. However, $\omega \not= [\omega + 1] $ as there can be no order preserving bijection ${ 0,1,2,\ldots } \rightarrow { 0,1,2,\ldots,0_{max} } $ as the first set has no maximal element whereas the second one does. So, Cantor’s addition has the bad property that it may be that $[\alpha + \beta] \not= [\beta + \alpha] $.
The Cantor-multiplication $ \alpha . \beta $ is the order-type of the product-set $\alpha \times \beta $ ordered via the last differing coordinate. Again, this product has the bad property that it may happen that $[\alpha . \beta] \not= [\beta . \alpha] $ (for example $[2 . \omega ] \not=[ \omega . 2 ] $). Finally, the exponential $\beta^{\alpha} $ is the order type of the set of all maps $f~:~\alpha \rightarrow \beta $ such that $f(a) \not=0 $ for only finitely many $a \in \alpha $, and ordered via the last differing function-value.
Cantor’s arithmetic allows normal-forms for ordinal numbers. More precisely, with respect to any ordinal number $\gamma \geq 2 $, every ordinal number $\alpha \geq 1 $ has a unique expression as
$\alpha = [ \gamma^{\alpha_0}.\eta_0 + \gamma^{\alpha_1}.\eta_1 + \ldots + \gamma^{\alpha_m}.\eta_m] $
for some natural number $m $ and such that $\alpha \geq \alpha_0 > \alpha_1 > \ldots > \alpha_m \geq 0 $ and all $1 \leq \eta_i < \gamma $. In particular, taking the special cases $\gamma = 2 $ and $\gamma = \omega $, we have the following two canonical forms for any ordinal number $\alpha $
$[ 2^{\alpha_0} + 2^{\alpha_1} + \ldots + 2^{\alpha_m}] = \alpha = [ \omega^{\beta_0}.n_0 + \omega^{\beta_1}.n_1 + \ldots + \omega^{\beta_k}.n_k] $
with $m,k,n_i $ natural numbers and $\alpha \geq \alpha_0 > \alpha_1 > \ldots > \alpha_m \geq 0 $ and $\alpha \geq \beta_0 > \beta_1 > \ldots > \beta_k \geq 0 $. Both canonical forms will be important when we consider the (better behaved) Conway-arithmetic on $\mathbf{On}_2 $, next time.
One Comment
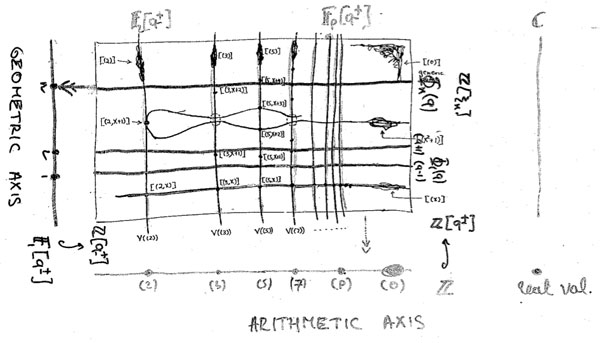
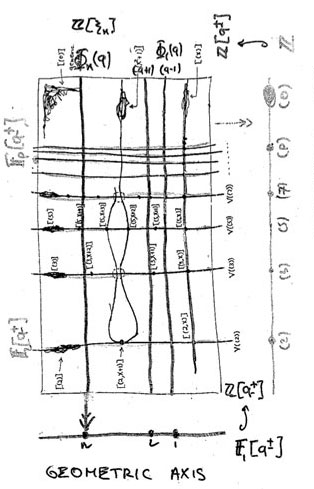

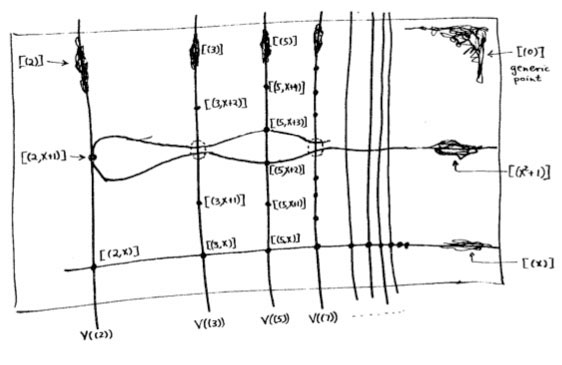
 The doodle in the right upper corner depicts the
The doodle in the right upper corner depicts the 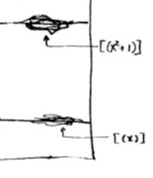 Let’s move over to the doodles in the lower right-hand corner. They represent the geometric object corresponding to principal prime ideals of the form $~(p(x)) $, where $p(x) $ in an
Let’s move over to the doodles in the lower right-hand corner. They represent the geometric object corresponding to principal prime ideals of the form $~(p(x)) $, where $p(x) $ in an  Apart from these ‘horizontal’ curves, there are also ‘vertical’ lines corresponding to the principal prime ideals $~(p) $, containing the polynomials, all of which coefficients are divisible by the prime number $p $. These are indeed prime ideals of $\mathbb{Z}[x] $, because their quotients are
Apart from these ‘horizontal’ curves, there are also ‘vertical’ lines corresponding to the principal prime ideals $~(p) $, containing the polynomials, all of which coefficients are divisible by the prime number $p $. These are indeed prime ideals of $\mathbb{Z}[x] $, because their quotients are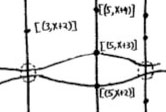 Right! So far we managed to depict the zero prime ideal (the whole plane) and the principal prime ideals of $\mathbb{Z}[x] $ (the horizontal curves and the vertical lines). Remains to depict the
Right! So far we managed to depict the zero prime ideal (the whole plane) and the principal prime ideals of $\mathbb{Z}[x] $ (the horizontal curves and the vertical lines). Remains to depict the