In his paper Cyclotomy and analytic geometry over $\mathbb{F}_1$ Yuri I. Manin sketches and compares four approaches to the definition of a geometry over $\mathbb{F}_1$, the elusive field with one element.
He writes : “Preparing a colloquium talk in Paris, I have succumbed to the temptation to associate them with some dominant trends in the history of art.”
Remember that the search for the absolute point $\pmb{spec}(\mathbb{F}_1)$ originates from the observation that $\pmb{spec}(\mathbb{Z})$, the set of all prime numbers together with $0$, is too large to serve as the terminal object in Grothendieck’s theory of commutative schemes. The last couple of years have seen a booming industry of proposals, to the extent that Javier Lopez Pena and Oliver Lorscheid decided they had to draw a map of $\mathbb{F}_1$-land.
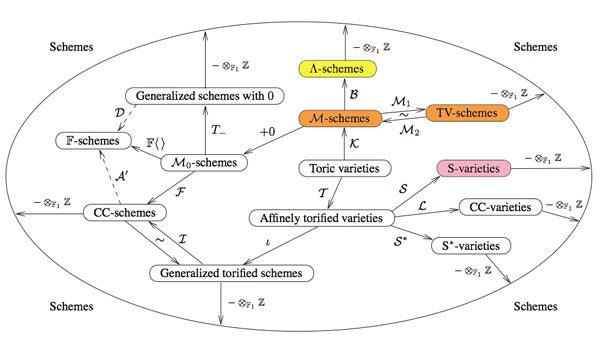
Manin only discusses the colored proposals (TV=Toen-Vaquie, M=Deitmar, S=Soule and $\Lambda$=Borger) and compares them to these art-history trends.
Toen and Vaquie : Abstract Expressionism
In Under $\pmb{spec}(\mathbb{Z})$ Bertrand Toen and Michel Vaquie argue that geometry over $\mathbb{F}_1$ is a special case of algebraic geometry over a symmetric monoidal category, taking the simplest example namely sets and direct products. Probably because of its richness and abstract nature, Manin associates this approach to Abstract Expressionism (a.o. Karel Appel, Jackson Pollock, Mark Rothko, Willem de Kooning).
Deitmar : Minimalism
Because monoids are the ‘commutative algebras’ in sets with direct products, an equivalent proposal is that of Anton Deitmar in Schemes over $\mathbb{F}_1$ in which the basic affine building blocks are spectra of monoids, topological spaces whose points are submonoids satisfying a primeness property. Because Deitmar himself calls this approach a ‘minimalistic’ one it is only natural to associate to it Minimalism where the work is stripped down to its most fundamental features. Prominent artists associated with this movement include Donald Judd, John McLaughlin, Agnes Martin, Dan Flavin, Robert Morris, Anne Truitt, and Frank Stella.
Soule : Critical Realism
in Les varietes sur le corps a un element Christophe Soule defines varieties over $\mathbb{F}_1$ to be specific schemes $X$ over $\mathbb{Z}$ together with a form of ‘descent data’ as well as an additional $\mathbb{C}$-algebra, morally the algebra of functions on the real place. Because of this Manin associates to it Critical Realism in philosophy. There are also ‘realism’ movements in art such as American Realism (o.a. Edward Hopper and John Sloan).
Borger : Futurism
James Borger’s paper Lambda-rings and the field with one element offers a totally new conception of the descent data from $\mathbb{Z}$ to $\mathbb{F}_1$, namely that of a $\lambda$-ring in the sense of Grothendieck. Because Manin expects this approach to lead to progress in the field, he connects it to Futurism, an artistic and social movement that originated in Italy in the early 20th century.
