Mark
Ronan has written a beautiful book intended for the general public
on Symmetry and the Monster. The
book’s main theme is the classification of the finite simple groups. It
starts off with the introduction of groups by Galois, gives the
classifivcation of the finite Lie groups, the Feit-Thompson theorem and
the construction of several of the sporadic groups (including the
Mathieu groups, the Fischer and Conway groups and clearly the
(Baby)Monster), explains the Leech lattice and the Monstrous Moonshine
conjectures and ends with Richard Borcherds proof of them using vertex
operator algebras. As in the case of Music of the
Primes it is (too) easy to be critical about notation. For example,
whereas groups are just called symmetry groups, I don’t see the point of
calling simple groups ‘atoms of symmetry’. But, unlike du Sautoy,
Mark Ronan stays close to mathematical notation, lattices are just
lattices, characer-tables are just that, j-function is what it is etc.
And even when he simplifies established teminology, for example
‘cyclic arithmetic’ for modular arithmetic, ‘cross-section’
for involution centralizer, ‘mini j-functions’ for Hauptmoduln
etc. there are footnotes (as well as a glossary) mentioning the genuine
terms. Group theory is a topic with several colourful people
including the three Johns John Leech, John
McKay and John Conway
and several of the historical accounts in the book are a good read. For
example, I’ve never known that the three Conway groups were essentially
discovered in just one afternoon and a few telephone exchanges between
Thompson and Conway. This year I’ve tried to explain some of
monstrous moonshine to an exceptionally good second year of
undergraduates but failed miserably. Whereas I somehow managed to give
the construction and proof of simplicity of Mathieu 24, elliptic and
modular functions were way too difficult for them. Perhaps I’ll give it
another (downkeyed) try using ‘Symmetry and the Monster’ as
reading material. Let’s hope Oxford University Press will soon release a
paperback (and cheaper) version.
Tag: Conway
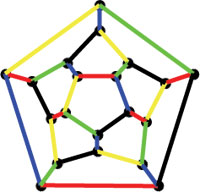
A _quintomino_ is a regular pentagon having all its sides
colored by five different colours. Two quintominoes are the same if they
can be transformed into each other by a symmetry of the pentagon (that
is, a cyclic rotation or a flip of the two faces). It is easy to see
that there are exactly 12 different quintominoes. On the other hand,
there are also exactly 12 pentagonal faces of a dodecahedron
whence the puzzling question whether the 12 quintominoes can be joined
together (colours mathching) into a dodecahedron.
According to
the Dictionnaire de
mathematiques recreatives this can be done and John Conway found 3
basic solutions in 1959. These 3 solutions can be found from the
diagrams below, taken from page 921 of the reprinted Winning Ways for your Mathematical
Plays (volume 4) where they are called _the_ three
quintominal dodecahedra giving the impression that there are just 3
solutions to the puzzle (up to symmetries of the dodecahedron). Here are
the 3 Conway solutions
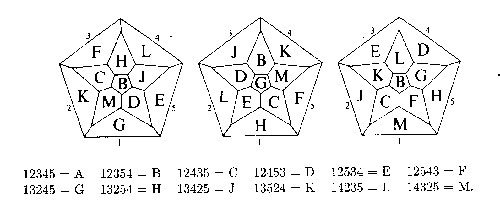
One projects the dodecahedron down from the top face which is
supposed to be the quintomino where the five colours red (1), blue (2),
yellow (3), green (4) and black(5) are ordered to form the quintomino of
type A=12345. Using the other quintomino-codes it is then easy to work
out how the quintominoes fit together to form a coloured dodecahedron.
In preparing to explain this puzzle for my geometry-101 course I
spend a couple of hours working out a possible method to prove that
these are indeed the only three solutions. The method is simple : take
one or two of the bottom pentagons and fill then with mathching
quintominoes, then these more or less fix all the other sides and
usually one quickly runs into a contradiction.
However, along the
way I found one case (see top picture) which seems to be a _new_
quintominal dodecahedron. It can't be one of the three Conway-types
as the central quintomino is of type F. Possibly I did something wrong
(but what?) or there are just more solutions and Conway stopped after
finding the first three of them…
Update (with help from
Michel Van den Bergh) Here is an elegant way to construct
'new' solutions from existing ones, take a permutation $\\sigma
\\in S_5$ permuting the five colours and look on the resulting colored
dodecahedron (which again is a solution) for the (new) face of type A
and project from it to get a new diagram. Probably the correct statement
of the quintominal-dodecahedron-problem is : find all solutions up to
symmetries of the dodecahedron _and_ permutations of the colours.
Likely, the 3 Conway solutions represent the different orbits under this
larger group action. Remains the problem : to which orbit belongs the
top picture??