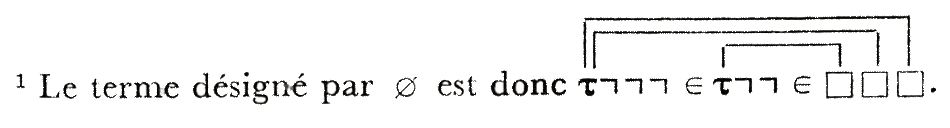“A story says that in a Paris café around 1955 Grothendieck asked his friends “what is a scheme?”. At the time only an undefined idea of “schéma” was current in Paris, meaning more or less whatever would improve on Weil’s foundations.” (McLarty in The Rising Sea)
Finding that particular café in Paris, presumably in the 5th arrondissement, seemed like looking for a needle in a haystack.
Until now.
In trying to solve the next riddle in Bourbaki’s death announcement:
A reception will be held at the Bar ‘The Direct Products’, at the crossroads of the Projective Resolutions (formerly Koszul square)
I’ve been reading Mathematics, a novel by Jacques Roubaud (the guy responsible for the announcement) on Parisian math-life in the 50ties and 60ties.
It turns out that the poor Bourbakistas had very little choice if they wanted to have a beer (or coffee) after attending a seminar at the IHP.
On page 114, Roubaud writes:
“Père Plantin presided over his bar, which presided over the Lhomond/Ulm street corner. It is an obvious choice. rue Pierre-et-Marie-Curie had no bars; rue d’Ulm had no bars in eyeshot either. If we emerged, as we did, on this side of the Institut Henri Poincaré (for doing so on the other side would have meant fraternizing with the Spanish and Geography students in the cafés on rue Saint-Jacques, which was out of the question), we had no choice. Café Plantin had a hegemony.”
It is unclear to me whether Plantin was once actually the name of the café, or that it’s just Roubaud’s code-word for it. At other places in the book, e.g. on pages 82 and 113, he consistently writes “Plantin”, between quotes.
Today, the café on the crossroads of rue d’Ulm (where the Ecole Normal Superieure is located) and de rue Lhomond is the Interlude Café

and here’s what Roubaud has to say about it, or rather about the situation in 1997, when the French version of his book was published:
“the thing that would currently be found at the very same corner of rues Lhomond/Ulm would not be what I am here terming “Plantin”.”
So, we can only hope that the Café ‘Aux Produits Directs’ was a lot cosier, way back then.
But let us return to Grothendieck’s “What is a scheme?” story.
Now that we have a fair idea of location, what about a possible date? Here’s a suggestion: this happened on monday december 12th, 1955, and, one of the friends present must have been Cartier.
Here’s why.
The very first time the word “schéma” was uttered, in Paris, at an official seminar talk, was during the Cartan seminar of 1955/56 on algebraic geometry.
The lecturer was Claude Chevalley, and the date was december 12th 1955.

I’m fairly certain Grothendieck and Cartier attended and that Cartier was either briefed before or understood the stuff at once (btw. he gave another talk on schemes, a year later at the Chevalley seminar).
A couple of days later, on december 15th, Grothendieck sends a letter to his pal Serre (who must have been out of Paris for otherwise they’d phone each other) ending with:

Note the phrase: I am exploiting him most profitably. Yes, by asking him daft questions over a pint at Café “Plantin”…
Leave a Comment A classic among mathematical jokes is the paper in the August/September 1938 issue of the American Mathematical Monthly “A contribution to the mathematical theory of big game hunting” by one Hector Petard of Princeton who would marry, one year later, Nicolas Bourbaki’s daughter Betti.
A classic among mathematical jokes is the paper in the August/September 1938 issue of the American Mathematical Monthly “A contribution to the mathematical theory of big game hunting” by one Hector Petard of Princeton who would marry, one year later, Nicolas Bourbaki’s daughter Betti.