Let’s try to identify the $\Psi(n) = n \prod_{p|n}(1+\frac{1}{p})$ points of $\mathbb{P}^1(\mathbb{Z}/n \mathbb{Z})$ with the lattices $L_{M \frac{g}{h}}$ at hyperdistance $n$ from the standard lattice $L_1$ in Conway’s big picture.
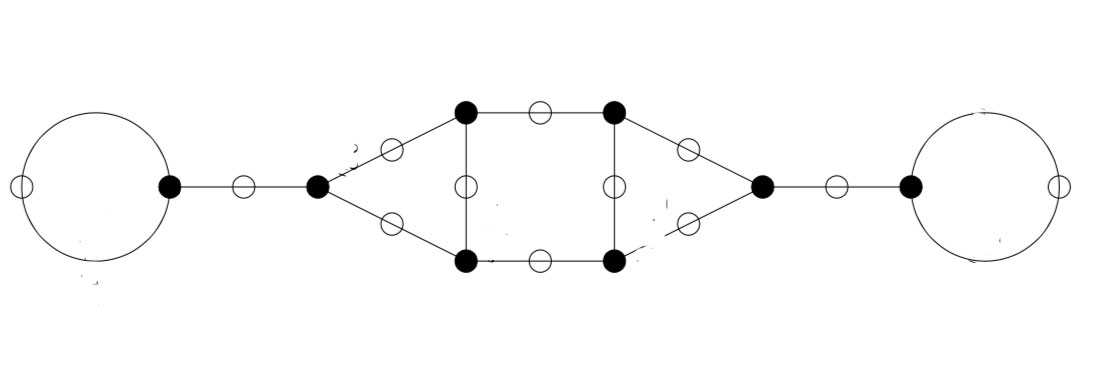
Here are all $24=\Psi(12)$ lattices at hyperdistance $12$ from $L_1$ (the boundary lattices):

You can also see the $4 = \Psi(3)$ lattices at hyperdistance $3$ (those connected to $1$ with a red arrow) as well as the intermediate $12 = \Psi(6)$ lattices at hyperdistance $6$.
The vertices of Conway’s Big Picture are the projective classes of integral sublattices of the standard lattice $\mathbb{Z}^2=\mathbb{Z} e_1 \oplus \mathbb{Z} e_2$.
Let’s say our sublattice is generated by the integral vectors $v=(v_1,v_2)$ and $w=(w_1.w_2)$. How do we determine its class $L_{M,\frac{g}{h}}$ where $M \in \mathbb{Q}_+$ is a strictly positive rational number and $0 \leq \frac{g}{h} < 1$?
Here’s an example: the sublattice (the thick dots) is spanned by the vectors $v=(2,1)$ and $w=(1,4)$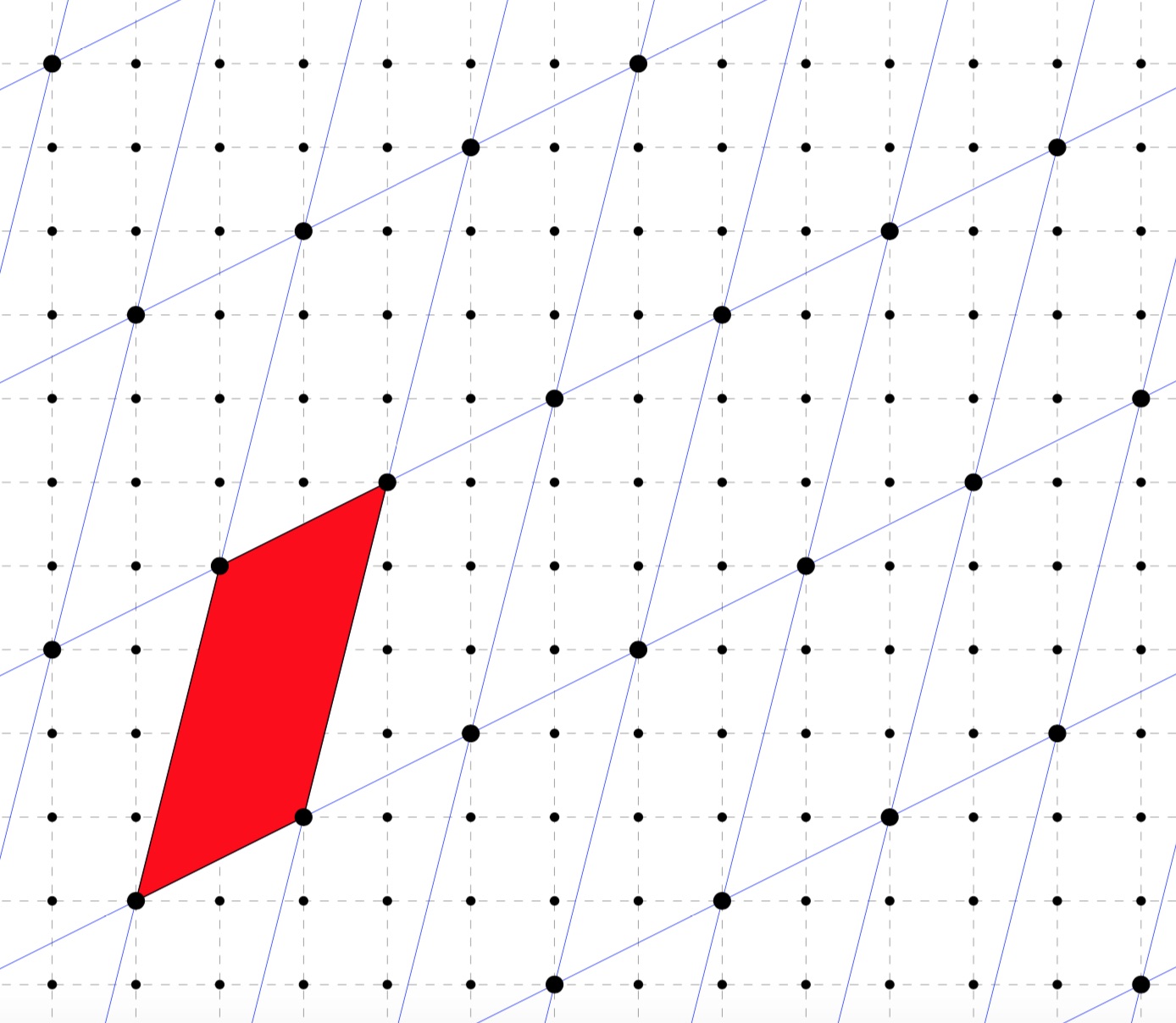
Well, we try to find a basechange matrix in $SL_2(\mathbb{Z})$ such that the new 2nd base vector is of the form $(0,z)$. To do this take coprime $(c,d) \in \mathbb{Z}^2$ such that $cv_1+dw_1=0$ and complete with $(a,b)$ satisfying $ad-bc=1$ via Bezout to a matrix in $SL_2(\mathbb{Z})$ such that
\[
\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} v_1 & v_2 \\ w_1 & w_2 \end{bmatrix} = \begin{bmatrix} x & y \\ 0 & z \end{bmatrix} \]
then the sublattice is of class $L_{\frac{x}{z},\frac{y}{z}~mod~1}$.
In the example, we have
\[
\begin{bmatrix} 0 & 1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 1 & 4 \end{bmatrix} = \begin{bmatrix} 1 & 4 \\ 0 & 7 \end{bmatrix} \]
so this sublattice is of class $L_{\frac{1}{7},\frac{4}{7}}$.
Starting from a class $L_{M,\frac{g}{h}}$ it is easy to work out its hyperdistance from $L_1$: let $d$ be the smallest natural number making the corresponding matrix integral
\[
d. \begin{bmatrix} M & \frac{g}{h} \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} u & v \\ 0 & w \end{bmatrix} \in M_2(\mathbb{Z}) \]
then $L_{M,\frac{g}{h}}$ is at hyperdistance $u . w$ from $L_1$.
Now that we know how to find the lattice class of any sublattice of $\mathbb{Z}^2$, let us assign a class to any point $[c:d]$ of $\mathbb{P}^1(\mathbb{Z}/n\mathbb{Z})$.
As $gcd(c,d)=1$, by Bezout we can find a integral matrix with determinant $1$
\[
S_{[c:d]} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]
But then the matrix
\[
\begin{bmatrix} a.n & b.n \\ c & d \end{bmatrix} \]
has determinant $n$.
Working backwards we see that the class $L_{[c:d]}$ of the sublattice of $\mathbb{Z}^2$ spanned by the vectors $(a.n,b.n)$ and $(c,d)$ is of hyperdistance $n$ from $L_1$.
This is how the correspondence between points of $\mathbb{P}^1(\mathbb{Z}/n\mathbb{Z})$ and classes in Conway’s big picture at hyperdistance $n$ from $L_1$ works.
Let’s do an example. Take the point $[7:3] \in \mathbb{P}^1(\mathbb{Z}/12\mathbb{Z})$ (see last time), then
\[
\begin{bmatrix} -2 & -1 \\ 7 & 3 \end{bmatrix} \in SL_2(\mathbb{Z}) \]
so we have to determine the class of the sublattice spanned by $(-24,-12)$ and $(7,3)$. As before we have to compute
\[
\begin{bmatrix} -2 & -7 \\ 7 & 24 \end{bmatrix} \begin{bmatrix} -24 & -12 \\ 7 & 3 \end{bmatrix} = \begin{bmatrix} -1 & 3 \\ 0 & -12 \end{bmatrix} \]
giving us that the class $L_{[7:3]} = L_{\frac{1}{12}\frac{3}{4}}$ (remember that the second term must be taken $mod~1$).
If you do this for all points in $\mathbb{P}^1(\mathbb{Z}/12\mathbb{Z})$ (and $\mathbb{P}^1(\mathbb{Z}/6\mathbb{Z})$ and $\mathbb{P}^1(\mathbb{Z}/3 \mathbb{Z})$) you get this version of the picture we started with
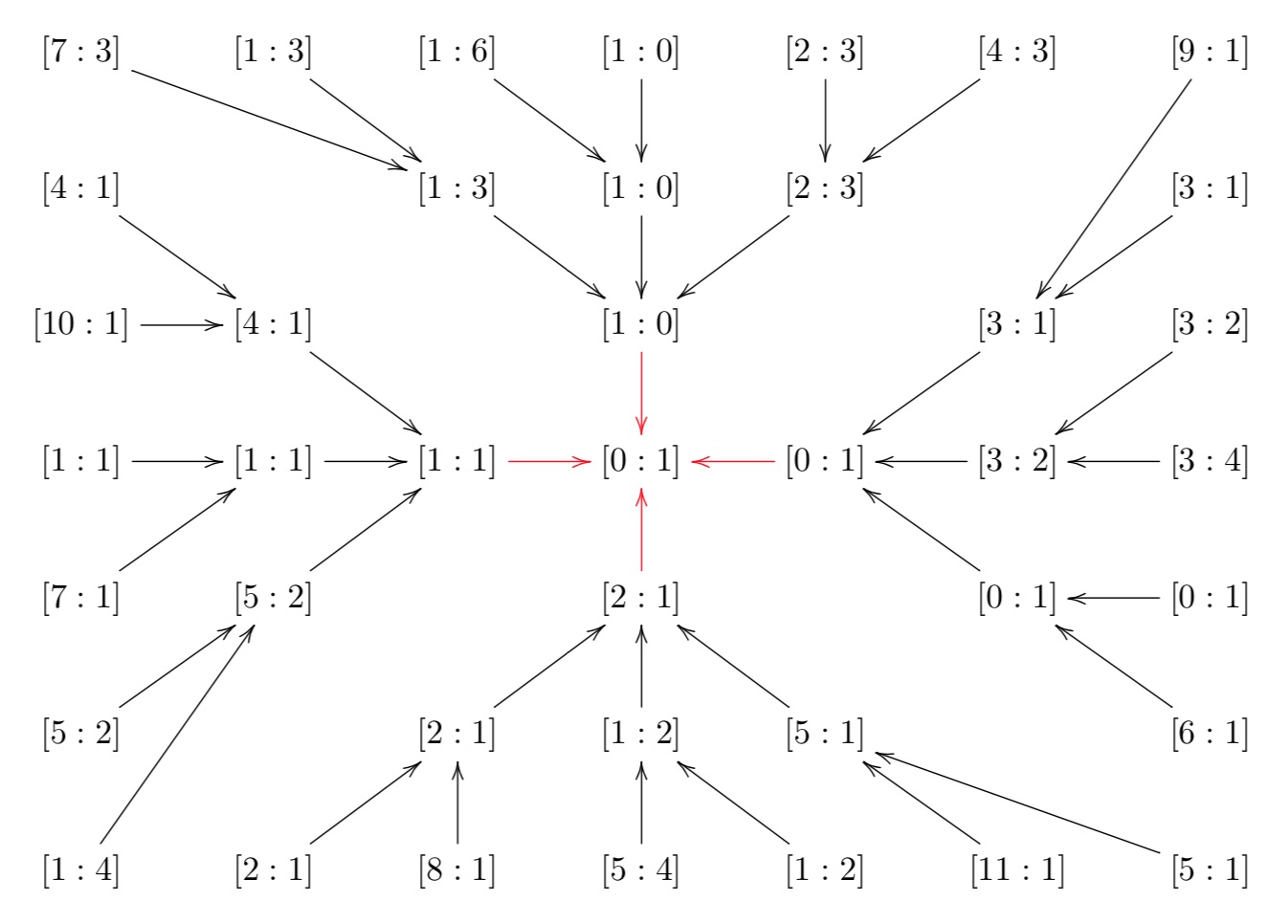
You’ll spot that the preimages of a canonical coordinate of $\mathbb{P}^1(\mathbb{Z}/m\mathbb{Z})$ for $m | n$ are the very same coordinate together with ‘new’ canonical coordinates in $\mathbb{P}^1(\mathbb{Z}/n\mathbb{Z})$.
To see that this correspondence is one-to-one and that the index of the congruence subgroup
\[
\Gamma_0(n) = \{ \begin{bmatrix} p & q \\ r & s \end{bmatrix}~|~n|r~\text{and}~ps-qr=1 \} \]
in the full modular group $\Gamma = PSL_2(\mathbb{Z})$ is equal to $\Psi(n)$ it is useful to consider the action of $PGL_2(\mathbb{Q})^+$ on the right on the classes of lattices.
The stabilizer of $L_1$ is the full modular group $\Gamma$ and the stabilizer of any class is a suitable conjugate of $\Gamma$. For example, for the class $L_n$ (that is, of the sublattice spanned by $(n,0)$ and $(0,1)$, which is of hyperdistance $n$ from $L_1$) this stabilizer is
\[
Stab(L_n) = \{ \begin{bmatrix} a & \frac{b}{n} \\ c.n & d \end{bmatrix}~|~ad-bc = 1 \} \]
and a very useful observation is that
\[
Stab(L_1) \cap Stab(L_n) = \Gamma_0(n) \]
This is the way Conway likes us to think about the congruence subgroup $\Gamma_0(n)$: it is the joint stabilizer of the classes $L_1$ and $L_n$ (as well as all classes in the ‘thread’ $L_m$ with $m | n$).
On the other hand, $\Gamma$ acts by rotations on the big picture: it only fixes $L_1$ and maps a class to another one of the same hyperdistance from $L_1$.The index of $\Gamma_0(n)$ in $\Gamma$ is then the number of classes at hyperdistance $n$.
To see that this number is $\Psi(n)$, first check that the classes at hyperdistance $p^k$ for $p$ a prime number and for all $k$ for the $p+1$ free valent tree with root $L_1$, so there are exactly $p^{k-1}(p+1)$ classes as hyperdistance $p^k$.
To get from this that the number of hyperdistance $n$ classes is indeed $\Psi(n) = \prod_{p|n}p^{v_p(n)-1}(p+1)$ we have to use the prime- factorisation of the hyperdistance (see this post).
The fundamental domain for the action of $\Gamma_0(12)$ by Moebius tranfos on the upper half plane must then consist of $48=2 \Psi(12)$ black or white hyperbolic triangles
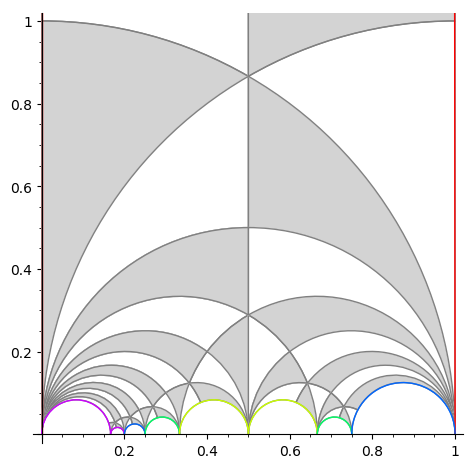
Next time we’ll see how to deduce the ‘monstrous’ Grothendieck dessin d’enfant for $\Gamma_0(12)$ from it