All lattices in the moonshine picture are number-like, that is of the form $M \frac{g}{h}$ with $M$ a positive integer and $0 \leq g < h$ with $(g,h)=1$. To understand the action of the Bost-Connes algebra on the Big Picture it is sometimes better to view the lattice $M \frac{g}{h}$ as a primitive $h$-th root of unity, centered at $hM$.
The distance from $M$ to any of the lattices $M \frac{g}{h}$ is equal to $2 log(h)$, and the distances from $M$ and $M \frac{g}{h}$ to $hM$ are all equal to $log(h)$.
For a prime value $h$, these $h$ lattices are among the $h+1$ lattices branching off at $hM$ in the $h$-adic tree (the remaining one being $h^2M$).
For general $h$ the situation is more complex. Here’s the picture for $h=6$ with edges in the $2$-adic tree painted blue, those in the $3$-adic tree red.
\[
\xymatrix{& & M \frac{1}{2} \ar@[blue]@{-}[d] & \\
& M \ar@[blue]@{-}[r] \ar@[red]@{-}[d] & 2M \ar@[red]@{-}[d] & M \frac{1}{6} \ar@[red]@{-}[d] \\
M \frac{1}{3} \ar@[red]@{-}[r] & 3M \ar@[blue]@{-}[r] \ar@[red]@{-}[d] & \boxed{6 M} \ar@[blue]@{-}[r] & 3M \frac{1}{2} \ar@[red]@{-}[d] \\ & M \frac{2}{3} & & M \frac{5}{6}} \]
To describe the moonshine group $(n|h)+e,f,\dots$ (an example was worked out in the tetrahedral snake post), we need to study the action of base-change with the matrix
\[
x = \begin{bmatrix} 1 & \frac{1}{h} \\ 0 & 1 \end{bmatrix} \]
which sends a lattice of the form $M \frac{g}{h}$ with $0 \leq g < h$ to $M \frac{g+M}{h}$, so is a rotation over $\frac{2 \pi M}{h}$ around $h M$.
But, we also have to describe the base-change action with the matrix
\[
y = \begin{bmatrix} 1 & 0 \\ n & 1 \end{bmatrix} \]
and for this we better use the second description of the lattice as $M \frac{g}{h}=(\frac{g'}{h},\frac{1}{h^2M})$ with $g'$ the multiplicative inverse of $g$ modulo $h$.
Under the action by $y$, the second factor $\frac{1}{h^2M}$ will be fixed, so this time we have to look at all lattices of the form $(\frac{g}{h},\frac{1}{h^2M})$ with $0 \leq g < h$, which again can be considered as another set of $h$-th roots of unity, centered at $hM$.
Here's this second interpretation for $h=6$:
\[
\xymatrix{M \frac{5}{6} \ar@[red]@{-}[d] & & 4M \frac{1}{3} \ar@[red]@{-}[d] & \\
3M \frac{1}{2} \ar@[blue]@{-}[r] \ar@[red]@{-}[d] & \boxed{6M} \ar@[blue]@{-}[r] \ar@[red]@{-}[d] & 12 M \ar@[red]@{-}[r] \ar@[red]@{-}[d] & 4 M \frac{2}{3} \\
M \frac{1}{6} & 18 M \ar@[blue]@{-}[r] \ar@[blue]@{-}[d] & 36 M & \\
& 9M \frac{1}{2} & & }
\]
Under $x$ the first set of $h$-th roots of unity centered at $hM$ is permuted, whereas $y$ permutes the second set of $h$-th roots of unity.
These interpretations can be used to spot errors in computing the finite groups $\Gamma_0(n|h)/\Gamma_0(n.h)$.
Here’s part of the calculation of the action of $y$ on the $(360|1)$-snake (which consists of $60$-lattices).
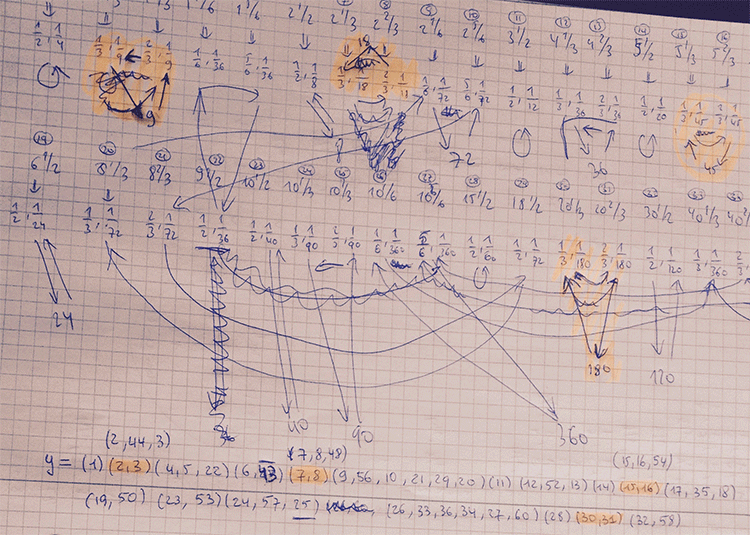
First I got a group of order roughly $600.000$. After correcting some erroneous cycles, the order went down to 6912.
Finally I spotted that I mis-numbered two lattices in the description of $x$ and $y$, and the order went down to $48$ as it should, because I knew it had to be equal to $C_2 \times C_2 \times A_4$.
Comments