Skip to content →

neverendingbooks Posts

On categories, go and the book $\in$

Published July 24, 2014 by lievenlb

A nice interview with Jacques Roubaud (the guy responsible for Bourbaki’s death announcement) in the courtyard of the ENS. He talks about go, categories, the composition of his book $\in$ and, of course, Grothendieck and Bourbaki.

Clearly there are pop-math books like dedicated to $\pi$ or $e$, but I don’t know just one novel having as its title a single mathematical symbol : $\in$ by Jacques Roubaud, which appeared in 1967.

The book consists of 361 small texts, 180 for the white stones and 181 for the black stones in a game of go, between Masami Shinohara (8th dan) and Mitsuo Takei (2nd Kyu). Here’s the game:

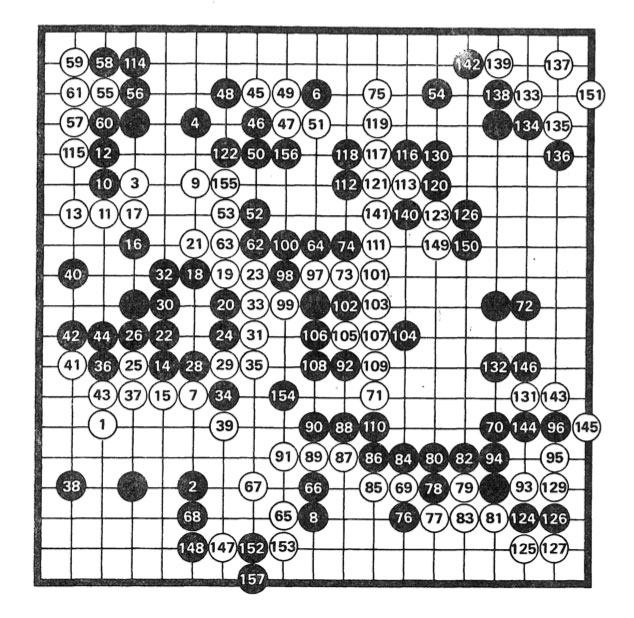
In the interview, Roubaud tells that go became quite popular in the mid sixties among French mathematicians, or at least those in the circle of Chevalley, who discovered the game in Japan and became a go-envangelist on his return to Paris.

In the preface to $\in$, the reader is invited to read it in a variety of possible ways. Either by paying attention to certain groupings of stones on the board, the corresponding texts sharing a common theme. Or, by reading them in order of how the go-game evolved (the numbering of white and black stones is not the same as the texts appearing in the book, fortunately there’s a conversion table on pages 153-155).

Or you can read them by paragraph, and each paragraph has as its title a mathematical symbol. We have $\in$, $\supset$, $\Box$, Hilbert’s $\tau$ and an imagined symbol ‘Symbole de la réflexion’, which are two mirrored and overlapping $\in$’s. For more information, thereader should consult the “Dictionnaire de la langue mathématique” by Lachatre and … Grothendieck.

According to the ‘bibliographie’ below it is number 17 in the ‘Publications of the L.I.T’.

Other ‘odd’ books in the list are: Bourbaki’s book on set theory, the thesis of Jean Benabou (who is responsible for Roubaud’s conversion from solving the exercises in Bourbaki to doing work in category theory. Roubaud also claims in the interview that category theory inspired him in the composition of the book $\in$) and there’s also Guillaume d’Ockham’s ‘Summa logicae’…

Leave a Comment

A noncommutative moduli space

Published July 19, 2014 by lievenlb

Supernatural numbers also appear in noncommutative geometry via James Glimm’s characterisation of a class of simple $C^*$-algebras, the UHF-algebras.

A uniformly hyperfine (or, UHF) algebra $A$ is a $C^*$-algebra that can be written as the closure, in the norm topology, of an increasing union of finite-dimensional full matrix algebras

$M_{c_1}(\mathbb{C}) \subset M_{c_2}(\mathbb{C}) \subset … \quad \subset A$

Such embedding are only possible if the matrix-sizes divide each other, that is $c_1 | c_2 | c_3 | … $, and we can assign to $A$ the supernatural number $s=\prod_i c_i$ and denote $A=A(s)$.

In his paper On a certain class of operator algebras, Glimm proved that two UHF-algebras $A(s)$ and $B(t)$ are isomorphic as $C^*$-algebras if and only if $s=t$. That is, the supernatural numbers $\mathbb{S}$ are precisely the isomorphism classes of UHF-algebras.

An important invariant, the Grothendieck group $K_0$ of $A(s)$, can be described as the additive subgroup $\mathbb{Q}(s)$ of $\mathbb{Q}$ generated by all fractions of the form $\frac{1}{n}$ where $n$ is a positive integer dividing $s$.

A “noncommutative space” is a Morita class of $C^*$-algebras, so we want to know when two $UHF$-algebras $A(s)$ and $B(t)$ are Morita-equivalent. This turns out to be the case when there are positive integers $n$ and $m$ such that $n.s = m.t$, or equivalently when the $K_0$’s $\mathbb{Q}(s)$ and $\mathbb{Q}(t)$ are isomorphic as additive subgroups of $\mathbb{Q}$.

Thus Morita-equivalence defines an equivalence relation on $\mathbb{S}$ as follows: if $s=\prod p^{s_p}$ and $t= \prod p^{t_p}$ then $s \sim t$ if and only if the following two properties are satisfied:

(1): $s_p = \infty$ iff $t_p= \infty$, and

(2): $s_p=t_p$ for all but finitely many primes $p$.

That is, we can view the equivalence classes $\mathbb{S}/\sim$ as the moduli space of noncommutative spaces associated to UHF-algebras!

Now, the equivalence relation is described in terms of isomorphism classes of additive subgroups of the rationals, which was precisely the characterisation of isomorphism classes of points in the arithmetic site, that is, the finite adèle classes

$\mathbb{S}/\sim~\simeq~\mathbb{Q}^* \backslash \mathbb{A}^f_{\mathbb{Q}} / \widehat{\mathbb{Z}}^*$

and as the induced topology of $\mathbb{A}^f_{\mathbb{Q}}$ on it is trivial, this “space” is usually thought of as a noncommutative space.

That is, $\mathbb{S}/\sim$ is a noncommutative moduli space of noncommutative spaces defined by UHF-algebras.

The finite integers form one equivalence class, corresponding to the fact that the finite dimensional UHF-algebras $M_n(\mathbb{C})$ are all Morita-equivalent to $\mathbb{C}$, or a bit more pompous, that the Brauer group $Br(\mathbb{C})$ is trivial.

Multiplication of supernaturals induces a well defined multiplication on equivalence classes, and, with that multiplication we can view $\mathbb{S}/\sim$ as the ‘Brauer-monoid’ $Br_{\infty}(\mathbb{C})$ of simple UHF-algebras…

(Btw. the photo of James Glimm above was taken by George Bergman in 1972)

Leave a Comment

Oulipo’s use of the Tohoku paper

Published July 17, 2014 by lievenlb

Many identify the ‘Tohoku Mathematical Journal’ with just one paper published in it, affectionately called the Tohoku paper: “Sur quelques points d’algèbre homologique” by Alexander Grothendieck.

In this paper, Grothendieck reshaped homological algebra for Abelian categories, extending the setting of Cartan-Eilenberg (their book and the paper both appeared in 1957). While working on the Tohoku paper in Kansas, Grothendieck did not have access to the manuscript of the 1956 book of Cartan-Eilenberg, about which he heard from his correspondence with Serre.

Concerning the title, an interesting suggestion was made by Mathieu Bélanger in his thesis “Grothendieck et les topos: rupture et continuité dans les modes d’analyse du concept d’espace topologique”, (footnote 18 on page 164):

“There is a striking resemblance between the title of the Grothendieck’s article “Sur quelques points d’algèbre homologique”, and that of Fréchet‘s thesis “Sur quelques points d’analyse fonctionelle”. Why? Grothendieck remains silent about it. Perhaps he saw a methodological similarity between the introduction, by Fréchet, of abstract spaces in order to develop the foundations of functional calculus and that of the Abelian categories he needed to clarify the homological theory. Compared with categories of sets, groups, topological spaces, etc. that were used until then, Abelian categories are in effect abstract categories.”

But, what does this have to do with the literary group OuLiPo (ouvroir de littérature potentielle, ‘workshop of potential literature’)?

Oulipo was founded in 1960 by Raymond Queneau and François Le Lionnais. Other notable members have included novelists Georges Perec and Italo Calvino, poets Oskar Pastior, Jean Lescure and poet/mathematician Jacques Roubaud.

Several members of Oulipo were either active mathematicians or at least had an interest in mathematics. Sometimes, Oulipo is said to be the literary answer to Bourbaki. The group explored new ways to create literature, often with methods coming from mathematics or programming.

One such method is described in “Chimères” by Le Lionnais:

One takes a source text A. One ’empties’ it, that is, one deletes all nouns, adjectives and verbs, but marks where they were in the text. In this way we have ‘prepared’ the text.

Next we take three target texts and make lists of words from them, K the list of nouns of the first, L the list of adjectives of the second and M the list of verbs of the third. Finally, we fill the empty spaces in the source text by words from the target lists, in the order that they appeared in the target texts.

In the example Le Lionnais gives, the liste M is the list of all verbs appearing in the Tohoku paper.


Leave a Comment