 In a few
In a few
weeks I will give a _geometry 101_ course! It was decided that in
this course I should try to explain what rotations in $\mathbb{R}^3’$
are, so the classification of all finite rotation groups seemed like a
fun topic. Along the way I’ll have to introduce groups so bringing in a
little bit of GAP
may be a good idea. Clearly, the real power of GAP is lost on the
symmetry groups of the Platonic solids so I’ll do the traditional
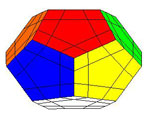
computation of the transformation group of the Rubik’s cube. But
then I discovered that there is also a version of it on the dodecahedron
which is called megaminx so I couldn’t resist trying to work out the order of its
transformation group. Fortunately Coreyanne Rickwalt did already the
hard work giving a presentation as
a permutation group. So giving the generators to GAP
f1:=(1,3,5,7,9)(2,4,6,8,10)(20,31,42,53,64)(19,30,41,52,63)(18,29,40,51,62);
f2:=(12,14,16,18,20)(13,15,17,19,21)(1,60,73,84,31)(3,62,75,86,23)(2,61,74,85,32);
f3:=(23,25,27,29,31)(24,26,28,30,32)(82,95,42,3,16)(83,96,43,4,17)(84,97,34,5,18);
f4:=(34,36,38,40,42)(35,37,39,41,43)(27,93,106,53,5)(28,94,107,54,6)(29,95,108,45,7);
f5:=(45,47,49,51,53)(46,48,50,52,54)(38,104,117,64,7)(39,105,118,65,8),(40,106,119,56,9);
f6:=(56,58,60,62,64)(57,59,61,63,65)(49,115,75,20,9)(50,116,76,21,10),(51,117,67,12,1);
f7:=(67,69,71,73,75)(68,70,72,74,76)(58,113,126,86,12)(59,114,127,7,13),(60,115,128,78,14);
f8:=(78,80,82,84,86)(79,81,83,85,87)(71,124,97,23,14)(72,125,98,24,15),(73,126,89,25,16);
f9:=(89,91,93,95,97)(90,92,94,96,98)(80,122,108,34,25)(81,123,109,35,26),(82,124,100,36,27);
f10:=(100,102,104,106,108)(101,103,105,107,109)(91,130,119,45,36),(92,131,120,46,37)(93,122,111,47,38);
f11:=(111,113,115,117,119)(112,114,116,118,120)(102,128,67,56,47),(103,129,68,57,48)(104,130,69,58,49);
f12:=(122,124,126,128,130)(123,125,127,129,131)(100,89,78,69,111),(101,90,79,70,112)(102,91,80,71,113);
and defining the
megaminx group by
megaminx:=Group(f1,f2,f3,f4,f5,f6,f7,f8,f9,f10,f11,f12); Size(megaminx);
and asking for its order I was a bit surprised to get
after a couple of minutes the following awkward number
33447514567245635287940590270451862933763731665690149051478356761508167786224814946834370826
35992490654078818946607045276267204294704060929949240557194825002982480260628480000000000000
000000000000000
or if you prefer it is
$2^{115} 3^{58} 5^{28} 7^{19} 11^{10} 13^9 17^7 19^6 23^5 29^4 31^3
37^3 41^2 43^2 47^2 53^2 59^2 61 .67 .71. 73. 79 .83 .89 .97. 101 .103.
107 .109 .113$