Yesterday around noon the former head of the local hunting society
turned up with our reward : a huge piece of the 110kg wild boar they
shot the day before.
A reward partly for taking care of the
two lost hunting dogs the day before (one of them was his but he is
missing another two dogs at the moment so we are asked to watch out for
them) partly because the hunters have to pass 'our land'.
Each year there is a “fete des chasseurs” to thank all
local people allowingh free passage during the hunt but it is scheduled
later in the year and we are not around at that time (come to think of
it, why not this year?).
In a previous post (I'll add
links later, I do not want to waste too much time on this dial-up
connection) I mentioned that this is the only way to get wild boar meat
around here. This time there was no trade-off involved but he would
accept “un cannon” (a glass of wine, rose in his case) or
two if we insisted.
To our surprise he sais that he hadn't
eaten wild boar for over 20 years… It seems that having to slice
up the meat after the hunt isn't appetizing. Here is how they divide
the meat after the hunt : they slice the boars up into pieces (last
week-end they shot 14 op tem in Sablieres alone) and divide the parts
into more or less equal heaps (as many as the number of people taking
part in the hunt).
Then, one of them is blindfolded and when
the others point to a heap the blinfolded person has to call out a name.
This process takes a while and is accompanied with quantities of Pastis
or wine.
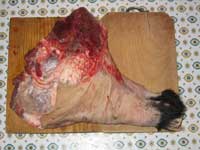
In previous years we got our meat nicely sliced up and packaged but
yesterday it was one huge lump of meat (probably a shoulder). So, I did
spend the better part of two hours slicing it up into pieces which is
pretty hard but indispensable work. I promised to prepare the boar by
wednesday evening (to be continued…).
 <
Monday morning 7 am : the first gunshots can be heard in the
distance. As the morning progresses they come closer and one can hear
the hunting dogs clearly. A bit later four or five white mini-vans
race up the road and turn to get to the ridge of the mountain, each
having one or more dogs inside. Fifteen minutes later, we have
eyesight contact with “les chasseurs” and the gunshots are
so nearby that one might consider taking cover … A typical
sunday in l'Ardeche-Cevenolle (I know, it is monday but yesterday
the weather was just too bad and luckily for them it's a holiday
today).
<
Monday morning 7 am : the first gunshots can be heard in the
distance. As the morning progresses they come closer and one can hear
the hunting dogs clearly. A bit later four or five white mini-vans
race up the road and turn to get to the ridge of the mountain, each
having one or more dogs inside. Fifteen minutes later, we have
eyesight contact with “les chasseurs” and the gunshots are
so nearby that one might consider taking cover … A typical
sunday in l'Ardeche-Cevenolle (I know, it is monday but yesterday
the weather was just too bad and luckily for them it's a holiday
today).