 How to sell
How to sell
modular arithmetic to students only interested in literature? Well, try
to explain the structure of ISBN-numbers
“The ISBN (International Standard Book Number) is a unique
machine-readable identification number, which marks any book
unmistakably. This number is defined in ISO Standard 2108. The number
has been in use now for 30 years and has revolutionised the
international book-trade. 166 countries and territories are officially
ISBN members. The ISBN accompanies a publication from its production
onwards.” The ISBN-number of a book is a ten-digit number divided into
four parts, separated by hyphens telling you a lot about the ambitions
and location of the book’ publisher. I’ll explain some of it by
telling how I obtained the barcode for the first book to be published by
neverendingbooks.org (see
picture). The first part is the group
identifier and identifies a country, area or language area
participating in the ISBN system. For the Netherlands and the Flemish
speaking part of Belgium this identifier is 90. Hence,
depending on your location you have to approach different agencies in
order to obtain an ISBN-number. If you are living in the US all you have
to do is to invent a name for your PublishingHouse, get your Visa-card
out and visit isbn.org
. For smaller groups the process is more personal. The first time I
tried to apply for an ISBN-number with De Boekenbank I
messed up and got immediately an email telling me what I did wrong. I
replied explaining what NeverEndingBooks had in mind and asked advice on
how to set it up properly. I’m sure I’ll need this personal contact
again in the near future. The second part is the _Publisher
Identifier_ or _prefix_. I didn’t know this before but the
very definition of a _publisher_ is the person or company
registering a book’s ISBN. Hence, if you intend to publish a series of
books your local ISBN-agency has to reserve a certain amount of
ISBN-numbers for you, all having the same start-block (the prefix). The
shorter the prefix the more ambitious the PublishingHouse. The
registered prefix of NeverEndingBooks is 90809390 which
tells the experienced ISBN-watcher that we intend in the next years to
publish “only” ten books. If you have more energy you can also apply
for a series of 100, 1000 or even 10000 ISBN-numbers but the amount of
money needed to register these series increases quickly… The third
part of the ISBN-number is the _title identifier_ so for our
first book it is just 1. However, in order to register
it you have to provide the agency (minimally) with a title and
publication date (fortunately, author, price, number of pages etc. are
optional at this stage). Anyway, the first real deadline for
NeverEndingBooks will be may 15th 2005! And now it is time to return
to modular arithmetic, the fourth part is a _check digit_. The
check digit is the last digit of an ISBN. It is calculated on a modulus
11 with weights 10-2, using X in lieu of 10 where ten would occur as a
check digit. This means that each of the first nine digits of the ISBN
excluding the check digit itself is multiplied by a number
ranging from 10 to 2 and that the resulting sum of the products, plus
the check digit, must be divisible by 11 without a remainder. In our
case, we have the following numbers(weights) 9(10) 0(9) 8(8)
0(7) 9(6) 3(5) 9(4) 0(3) 1(2) We have to multiply the numbers
with their weight and add them all up,
90+0+64+0+54+15+36+0+2=261=8(mod 11) whence the check
digit should be 3. For example, I know already that the
ISBN-number of the second book to be published by NeverEndingBooks will
be 90-809390-2-1 but, due to lacking information, it will take a while
before it can be registered.
neverendingbooks Posts

It is far from finished but you can already visit a demo-version of
TheLibrary which I hope will one day be a useful collection of
online courses and books on non-commutative algebra & geometry. At
the moment it just contains a few of my own things but I do hope that
others will find the format interesting enough to allow me to include
their courses and/or books. So, please try this demo out! But before you
do, make sure that you have a good webbrowser-plugin to view
PDF-documents from within your browser (rather than having to download
the files). If you are using Macintosh 10.3 or better there is a very
nice plugin freely
available whch you only have to drag into your _/Library/Internet
Plug-Ins/_-folder to get it working (after restarting Safari).
If you click on the title you will get a page with hyper-links to all
bookmarks of the pdf-file (for example, if you have used the hyperref package to
(La)TeX your file, you get these bookmarks for free). If you only have a
PDF-file you can always include the required bookmarks using Acrobat.
No doubt the most useful feature (at this moment) of the set-up is
that all files are fully searchable for keywords.
For example, if
you are at the page of my 3 talks on noncommutative
geometry@n-course and fill out “Azumaya” in the Search
Document-field you will get a screen like the one below
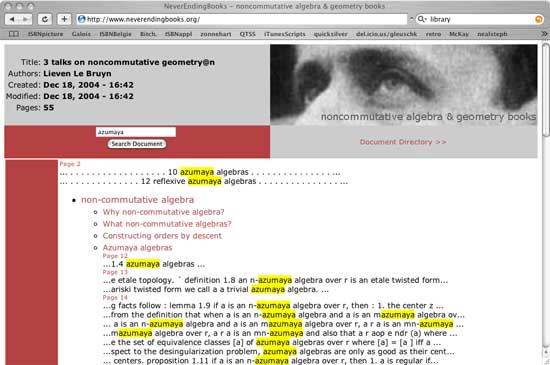
That is, you wlll get all occurrences of 'Azumaya' in
the document together with some of the context as well as page- or
section-links nearby that you can click to get to the paragraph you are
looking for. In the weeks to come I hope to extend the usability of
_TheLibrary_ by offering a one-page view, modular security
enhancements, a commenting feature as well as a popularity count. But,
as always, this may take longer than I want…
If you think
that the present set-up might already be of interest to readers of your
courses or books and if you have a good PDF-file of it available
(including bookmarks) then email and we will try to include your
material!

Evariste Galois (1811-1832) must rank pretty high on the all-time
list of moving last words. Galois was mortally wounded in a duel he
fought with Perscheux d\’Herbinville on May 30th 1832, the reason for
the duel not being clear but certainly linked to a girl called
Stephanie, whose name appears several times as a marginal note in
Galois\’ manuscripts (see illustration). When he died in the arms of his
younger brother Alfred he reportedly said “Ne pleure pas, j\’ai besoin
de tout mon courage pour mourir ‚àö‚Ć 20 ans”. In this series I\’ll
start with a pretty concrete problem in Galois theory and explain its
elegant solution by Aidan Schofield and Michel Van den Bergh.
Next, I\’ll rephrase the problem in non-commutative geometry lingo,
generalise it to absurd levels and finally I\’ll introduce a coalgebra
(yes, a co-algebra…) that explains it all. But, it will take some time
to get there. Start with your favourite basefield $k$ of
characteristic zero (take $k = \mathbb{Q}$ if you have no strong
preference of your own). Take three elements $a,b,c$ none of which
squares, then what conditions (if any) must be imposed on $a,b,c$ and $n
\in \mathbb{N}$ to construct a central simple algebra $\Sigma$ of
dimension $n^2$ over the function field of an algebraic $k$-variety such
that the three quadratic fieldextensions $k\sqrt{a}, k\sqrt{b}$ and
$k\sqrt{c}$ embed into $\Sigma$? Aidan and Michel show in \’Division
algebra coproducts of index $n$\’ (Trans. Amer. Math. Soc. 341 (1994),
505-517) that the only condition needed is that $n$ is an even number.
In fact, they work a lot harder to prove that one can even take $\Sigma$
to be a division algebra. They start with the algebra free
product $A = k\sqrt{a} \ast k\sqrt{b} \ast k\sqrt{c}$ which is a pretty
monstrous algebra. Take three letters $x,y,z$ and consider all
non-commutative words in $x,y$ and $z$ without repetition (that is, no
two consecutive $x,y$ or $z$\’s). These words form a $k$-basis for $A$
and the multiplication is induced by concatenation of words subject to
the simplifying relations $x.x=a,y.y=b$ and $z.z=c$.
Next, they look
at the affine $k$-varieties $\mathbf{rep}(n) A$ of $n$-dimensional
$k$-representations of $A$ and their irreducible components. In the
parlance of $\mathbf{geometry@n}$, these irreducible components correspond
to the minimal primes of the level $n$-approximation algebra $\int(n) A$.
Aidan and Michel worry a bit about reducedness of these components but
nowadays we know that $A$ is an example of a non-commutative manifold (a
la Cuntz-Quillen or Kontsevich-Rosenberg) and hence all representation
varieties $\mathbf{rep}n A$ are smooth varieties (whence reduced) though
they may have several connected components. To determine the number of
irreducible (which in this case, is the same as connected) components
they use _Galois descent, that is, they consider the algebra $A
\otimes_k \overline{k}$ where $\overline{k}$ is the algebraic closure of
$k$. The algebra $A \otimes_k \overline{k}$ is the group-algebra of the
group free product $\mathbb{Z}/2\mathbb{Z} \ast \mathbb{Z}/2\mathbb{Z}
\ast \mathbb{Z}/2\mathbb{Z}$. (to be continued…) A digression : I
cannot resist the temptation to mention the tetrahedral snake problem
in relation to such groups. If one would have started with $4$ quadratic
fieldextensions one would get the free product $G =
\mathbb{Z}/2\mathbb{Z} \ast \mathbb{Z}/2\mathbb{Z} \ast
\mathbb{Z}/2\mathbb{Z} \ast \mathbb{Z}/2\mathbb{Z}$. Take a supply of
tetrahedra and glue them together along common faces so that any
tertrahedron is glued to maximum two others. In this way one forms a
tetrahedral-snake and the problem asks whether it is possible to make
such a snake having the property that the orientation of the
\’tail-tetrahedron\’ in $\mathbb{R}^3$ is exactly the same as the
orientation of the \’head-tetrahedron\’. This is not possible and the
proof of it uses the fact that there are no non-trivial relations
between the four generators $x,y,z,u$ of $\mathbb{Z}/2\mathbb{Z} \ast
\mathbb{Z}/2\mathbb{Z} \ast \mathbb{Z}/2\mathbb{Z} \ast
\mathbb{Z}/2\mathbb{Z}$ which correspond to reflections wrt. a face of
the tetrahedron (in fact, there are no relations between these
reflections other than each has order two, so the subgroup generated by
these four reflections is the group $G$). More details can be found in
Stan Wagon\’s excellent book The Banach-tarski paradox, p.68-71.