Let us
begin with a simple enough question : what are the points of a
non-commutative variety? Anyone? Probably you\’d say something like :
standard algebra-geometry yoga tells us that we should associate to a
non-commutative algebra $A$ on object, say $X_A$ and an arbitrary
variety is then build from \’gluing\’ such things together. Ok, but what
is $X_A$? Commutative tradition whispers $X_A=\mathbf{spec}~A$ the
[prime spectrum][1] of $A$, that is, the set of all twosided prime
ideals $P$ (that is, if $aAb \subset P$ then either $a \in P$ or $b \in
P$) and \’points\’ of $\mathbf{spec}~A$ would then correspond to
_maximal_ twosided ideals. The good news is that in this set-up, the
point-set comes equipped with a natural topology, the [Zariski
topology][2]. The bad news is that the prime spectrum is rarely
functorial in the noncommutative world. That is, if $\phi~:~A
\rightarrow B$ is an algebra morphism then $\phi^{-1}(P)$ for $P \in
\mathbf{spec}~B$ is not always a prime ideal of $A$. For example, take
$\phi$ the inclusion map $\begin{bmatrix} C[x] & C[x] \\ (x) & C[x]
\end{bmatrix} \subset \begin{bmatrix} C[x] & C[x] \\ C[x] & C[x]
\end{bmatrix}$ and $P$ the prime ideal $\begin{bmatrix} (x) & (x) \\ (x)
& (x) \end{bmatrix}$ then $P Cap \begin{bmatrix} C[x] & C[x] \\ (x) &
C[x] \end{bmatrix} = P$ but the corresponding quotient is
$\begin{bmatrix} C & C \\ 0 & C \end{bmatrix}$ which is not a prime
algebra so $\phi^{-1}(P)$ is not a prime ideal of the smaller algebra.
Failing this, let us take for $X_A$ something which obviously is
functorial and worry about topologies later. Take $X_A = \mathbf{rep}~A$
the set of all finite dimensional representations of $A$, that is
$\mathbf{rep}~A = \bigsqcup_n \mathbf{rep}_n~A$ where $\mathbf{rep}_n~A
= \{ Chi~:~A \rightarrow M_n(C)~\}$ with $Chi$ an algebra morphism. Now,
for any algebra morphism $\phi~:~A \rightarrow B$ there is an obvious
map $\mathbf{rep}~B \rightarrow \mathbf{rep}~A$ sending $Chi \mapsto Chi
Circ \phi$. Alernatively, $\mathbf{rep}_n~A$ is the set of all
$n$-dimensional left $A$-modules $M_{Chi} = C^n_{Chi}$ with $a.m =
Chi(m)m$. As such, $\mathbf{rep}~A$ is not merely a set but a
$C$-_category_, that is, all objects are $C$-vectorspaces and all
morphisms $Hom(M,N)$ are $C$-vectorspaces (the left $A$-module
morphisms). Moreover, it is an _additive_ category, that is if
$Chi,\psi$ are representations then we also have a direct sum
representation $Chi \oplus \psi$ defined by $a \mapsto \begin{bmatrix}
Chi(a) & 0 \\ 0 & \psi(a) \end{bmatrix}$. Returning at the task at
hand let us declare a _non-commutative variety_ $X$ to be (1) _an
additive_ $C$-_category_ which \’locally\’ looks like $\mathbf{rep}~A$
for some non-commutative algebra $A$ (even if we do not know at the
momemt what we mean by locally as we do not have defined a topology,
yet). Let is call objects of teh category $X$ the \’points\’ of our
variety and $X$ being additive allows us to speak of _indecomposable_
points (that is, those objects that cannot be written as a direct sum of
non-zero objects). By the local description of $X$ an indecomposable
point corresponds to an indecomposable representation of a
non-commutative algebra and as such has a local endomorphism algebra
(that is, all non-invertible endomorphisms form a twosided ideal). But
if we have this property for all indecomposable points,our category $X$
will be a Krull-Schmidt category so it is natural to impose also the
condition (2) : every point of $X$ can be decomposed uniquely into a
finite direct sum of indecomposable points. Further, as the space of
left $A$-module morphisms between two finite dimensional modules is
clearly finite dimensional we have also the following strong finiteness
condition (3) : For all points $x,y \in X$ the space of morphisms
$Hom(x,y)$ is a finite dimensional $C$-vectorspace. In their book
[Representations of finite-dimensional algebras][3], Peter Gabriel and
Andrei V. Roiter call an additive category such that all endomorphism
algebras of indecomposable objects are local algebras and such that all
morphism spaces are finite dimensional an _aggregate_. So, we have a
first tentative answer to our question **the points of a
non-commutative variety are the objects of an aggregate** Clearly, as
$\mathbf{rep}~A$ has stronger properties like being an _Abelian
category_ (that is, morphisms allow kernels and cokernels) it might also
be natural to replace \’aggregate\’ by \’Abelian Krull-Schmidt category
with finite dimensional homs\’ but if Mr. Abelian Category himself finds
the generalization to aggregates useful I\’m not going to argue about
this. Are all aggregates of the form $\mathbf{rep}~A$ or are there
other interesting examples? A motivating commutative example is : the
category of all coherent modules $Coh(Y)$ on a _projective_ variety $Y$
form an aggegate giving us a mental picture of what we might expect of a
non-commutative variety. Clearly, the above tentative answer cannot be
the full story as we haven\’t included the topological condition of
being locally of the form $\mathbf{rep}~A$ yet, but we will do that in
the next episode _B for Bricks_. [1]:
http://planetmath.org/encyclopedia/PrimeSpectrum.html [2]:
http://planetmath.org/encyclopedia/ZariskiTopology.html [3]:
1/ref=sr_1_8_1/026-3923724-4530018
neverendingbooks Posts

Just in time for 2005 : a pretty good approx of what I had in mind
with TheLibrary.
The major new feature is one-page view. That
is, if you click on a bookmark or search-page link you will get a page
(as in the screenshot below) consisting of three frames. The left-bottom
frame contains the pdf file of _just_ the requested page, hence
your brwoser no longer has to download the full pdf-file to get at the
wanted page which speeds up the process. The downside is that you can no
longer scroll in neighbouring pages. To compensate for this there are
_previous page_ and _next page_ buttons in the top frame
as well as a link to the index and search page of the document.
An added bonus of this set-up is that the author of a document can
control what readers can do with these pdf-pages. For example, the pages
of 3 talks on noncommutative geometry@n
admit all features (such as content-copy, merging pages, printing etc.)
whence a determined reader can reconstruct the full pdf-document if
he/she so desires. On the other hand, the pages of version 2 can only be printed at a low
resolution and those of version 3 do not even permit this.
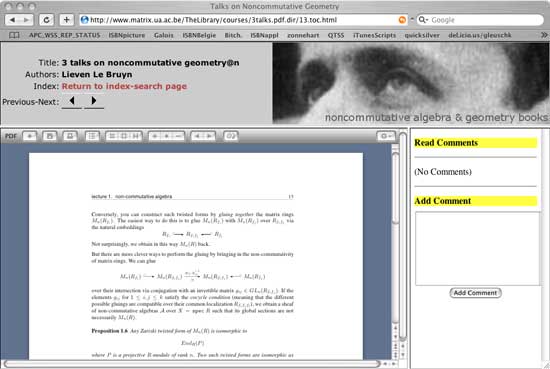
The bottom-right frame of the pages allow the reader
to read (and post) marginal notes wrt. the content of the document-text
(such as : extra references, errors, suggestions etc.). As always,
comments are great; obnoxious comments get deleted. Deal!
Once
again, if you like your courses and or books (on a subject from either
non-commutative geometry or non-commutative algebra) to be included in
TheLibrary email.
All scripts are adapted from the original
scripts from pdf
hacks.

This is the first version of a set of general frequently asked
questions relating to _NeverEndingBooks_. An extended and updated
version of it is at all times available from the sidebar under the
heading 'FAQ'. If you have a question and/or suggestion for
these FAQs, please email and it will be answered/used in an updated
version.
What is NeverEndingBooks ?
neverendingbooks.org is a
non-profit PublishingHouse specializing in courses and books on
non-commutative algebra and/or non-commutative geometry. Our authors
have a set of notes on a subject in na&g and hope to turn it into a
book one fine day. We offer them help throughout this process, from
secure on-screen viewing & commenting of their successive versions
to the production of a genuine hardcopy version distributed worldwide.
At all times we aim to keep the costs of our books minimal and the
royalties & copyrights for our authors maximal.
NeverEndingBooks' coordinates are :
NeverEndingBooks.org
c/o Lieven Le Bruyn
Department Mathematics UA
Middelheimlaan 1
B-2020 Antwerp, Belgium
URL : www.neverendingbooks.org
ISBN-prefix : 90-809390
Why NeverEndingBooks
?
We all complain about exaggerated prices of
mathematical books from certain publishers, poor quality of editing and
refereeing offered as well as far too stringent book-contracts. Rather
than lamenting about this, NeverEndingBooks gives itself one year to
learn (and report) about the many aspects of the book-production cyclus
and to explore whether an alternative exists. If at the end of this year
we will have produced at least one book this experiment will be
considered a success. If, however, we find out that it is an impossible
task, we will explain where it all went wrong and why it is better to
stick to an established PublishingHouse and accept its terms.