I have
been posting before on the necklace Lie algebra : on Travis
Schedler's extension of the Lie algebra structure to a Lie bialgebra
and its deformation and more recently
in connection with Michel Van den Bergh's double Poisson paper.
Yesterday, Victor Ginzburg and Travis Schedler posted their paper Moyal quantization of
necklace Lie algebras on the arXiv in which they give a Moyal-type
construction of the Hopf algebra deformation of the necklace Lie
bialgebra found by Schedler last year.
It would be nice if
someone worked out a few examples of these constructions in full detail.
But as often in the case of (wild) quiver situation it is not clear what
an 'interesting' example might be. For the finite and tame case
we have a full classification by (extended) Dynkin diagrams so a natural
class of examples but it isn't clear how to find gems in the
complement.
One natural source of double quiver situations seems
to come from what I called the One Quiver of a
formally smooth algebra. This one quiver of group algebras of some
interesting arithemetical groups such as the modular group
$PSL_2(\mathbb{Z}) $ and $SL_2(\mathbb{Z}) $ were calculated before and
turned out to be consisting of one (resp. two) components which are the
double of the tame quiver $\tilde{A}_5 $.
To obtain the double of
a wild quiver situation loook at the group $GL_2(\mathbb{Z}) = D_4
\bigstar_{D_2} D_6 $. In a previous post
I thought to have calculated it, but lately I found that this was
incorrect. Even the version I computed last week still had some mistakes
as Raf
Bocklandt discovered. But as of yesterday we are pretty certain that
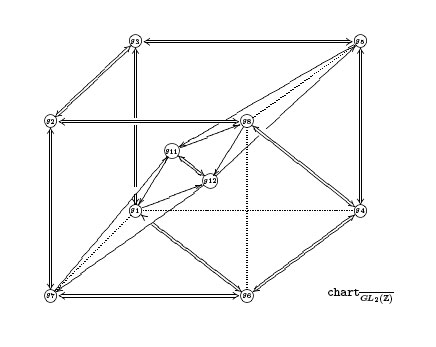
the one quiver for $GL_2(\mathbb{Z}) $ consists of two components. One of
these is the double quiver of an interesting wild quiver
$\xymatrix{& \vtx{} \ar@{=}[rr] \ar@{=}[dd] & & \vtx{} \ar@{=}[dd]
\\ \vtx{} \ar@{=}[ur] \ar@{=}[rr] \ar@{=}[dd] & & \vtx{} \ar@{.}[ur]
\ar@{.}[dd] \ar@{=}[dr] \\ & \vtx{} \ar@{.}[rr] \ar@{=}[dr] & & \vtx{}
\\ \vtx{} \ar@{=}[rr] \ar@{.}[ur] & & \vtx{} \ar@{=}[ur]} $
where each double line indicates that there is an arrow in each
direction between the vertices. So, it is an interwoven pattern of one
big cycle of length 6 (reminiscent of the modular group case) with 4
cycles of length 5. Perhaps the associated necklace Lie (bi)algebra and
its deformation might be interesting to work out.
However, the
second component of the one quiver for $GL_2(\mathbb{Z}) $ is _not_
symmetric.Maybe I will come back to the calculation of these quivers
later.