My Google+ account is going away on April 2, 2019, so i’ll try to rescue here some posts, in chronological order and around one theme. Here’s Grothendieck-stuff, part two.
March 18th, 2014
crowd-funding Grothendiecks biography?
+John Baez has a post out at the n-cat-cafe on Leila Schneps’s quest to raise $6000 to translate Scharlau’s 3-volume biography of Grothendieck.
If you care to contribute : go here.
Lots of good stuff in volume 3 on Groths hippy/eco/weirdo years. I’ve plundered Scharlau’s text last year trying to pinpoint the location of Groths hideout in the French Pyrenees.
As far as i know, part 2 (the most interesting part on Groths mathematical years) is still under construction and will be compiled by the jolly group called the “Grothendieck circle”.
There’s a nice series of G-recollections out here (a.o. by Illusie, Karoubi, Cartier, Raynaud, Mumford, Hartshorne, Murre, Oort, Manin, Cartier).
I’m pretty sure Groth himself would prefer we’d try to get his Recoltes et Semailles translated into English, or La Clef des Songes.
November 18th, 2014
Grothendieck’s last hideout
The past ten days I’ve been up in the French mountains (without internet access), not that far from the Ariege, so I’m just now catching up with all (blog)posts related to Grothendieck’s death.
At our place, the morning of thursday november 13th was glorious!

Even though FranceInter kept telling horror stories about flooding in more southern departements, I can only hope that Grothendieck passed away in that morning sun.
About a year ago, on the occasion of Groth’s 85th birthday, I ran a series of posts on places where he used to live, ending with his last known hideout
At the time I didn’t include the precise location of his house, but now that pictures of it are in the French press I feel free to suggest (if you are interested to know where Grothendieck spend his later years) to point your Google-earth or Google-maps (in streetview!) to:
lat 43.068254 lon 1.169080
November 18th, 2014
Mormoiron and Lasserre acknowledge Grothendieck
In the series of post on Grothendieck-places I wrote a year ago (see here and links at the end) I tried to convince these French villages to update their Wikipedia page to acknowledge the existence of Grothendieck under the heading ‘Personnalités liées à la commune’, without much success.
Today it is nice to see that Lasserre added Grothendieck to their page:
“Alexandre Grothendieck (1928-2014), considéré comme un des plus grands mathématiciens du xxe siècle, y a vécu en quasi-ermite de 1990 à sa mort.”
Also Mormoiron, where Grothendieck lived in the 80ties (see picture below) has updated its page:
“Alexandre Grothendieck a habité temporairement à Mormoiron (“Les Aumettes”)”

French villages who still have to follow suit:
– Vendargues
– Massy
– Olmet-et-Villecun
November 19th, 2014
Please keep an eye on the GrothendieckCircle for updates
+Leila Schneps invested a lot of time over the years setting up the Grothendieck Circle website.
Some material had to be removed a few years ago as per Groth’s request.
I’m sure many of you will be as thrilled as I was to get this message from Leila:
“I have already started modifying the Grothendieck circle website and it will of course eventually return completely. Plus many things will be added, as we will now have access to Grothendieck’s correspondence and many other papers.”
Leila already began to update the site, for example there’s this new page on Groth’s life in Lasserre.
I understand Leila is traveling to Lasserre tomorrow, presumably for Grothendieck’s funeral. Hopefully she will eventually post something about it on the GrothendieckCircle (or, why not here on G+).
December 4th, 2014
Nicolas Bourbaki is temporarily resurrected to announce the death of Grothendieck in the French newspaper Le Monde.
You may recall that Bourbaki passed away on november 11th 1968, see +Peter Luschny’s post on his death announcement.

December 6th, 2014
The ‘avis de décès’ released by Grothendieck’s family and friends, published in the local French newspaper ‘La Depeche’, on saturday november 15th.
It announces Grothendieck’s cremation, on november 17th at 11.30h in the village of Pamiers, bordering the ‘Camp du Vernet’, where Grothendieck’s father Sasha was imprisoned, before being deported to Auschwitz and murdered by the Nazis in 1942.

June 12th, 2015
Grothendieck’s later writings
Next week there’s a Grothendieck conference at Montpellier. George Maltsiniotis will give a talk thursday afternoon with the exciting title “Grothendieck’s manuscripts in Lasserre” (hat tip +Pieter Belmans ).
You may recall that G’s last hideout was in the Pyrenean village of Lasserre.
After a bit of sleuthing around I’ve heard some great news.
Grothendieck’s family have donated all of his later writings (apart from his correspondences and other family-related stuff) to the Bibliotheque Nationale. The BNF have expressed their intention of scanning all this material (thousands of pages it seems) and making them (eventually) available online!
Rumour has it that the donation consists of 41 large folders containing G’s reflections, kept in the form of a diary (a bit like ‘Clef des Songes’), on G’s usual suspects (evil, Satan, the cosmos), but 2 or 3 of these folders contain mathematics (of sorts).
Probably, Maltsiniotis will give a preview on this material. To anyone lucky enough to be able to go down south next week and to attend his talk, please keep me in the loop…

June 19th, 2015
Maltsiniotis’ talk on Grothendieck’s Lasserre-gribouillis
Yesterday, George Maltsiniotis gave a talk at the Gothendieck conference in Montpellier with title “Grothendieck’s manuscripts in Lasserre”.
This morning, +David Roberts asked for more information on its content, and earlier i gave a short reply on what i learned, but perhaps this matter deserves a more careful write-up.
+Damien Calaque attended George’s talk and all info below is based on his recollections. Damien stresses that he didn’t take notes so there might be minor errors in the titles and order of the parts mentioned below.
EDIT: based on info i got from +Pieter Belmans in the comments below (followed up by the picture he got via +Adeel Khan taken by Edouard Balzin) i’ve corrected the order and added additional info.
The talk was videotaped and should become public soon.
As i mentioned last week Grothendieck’s family has handed over all non-family related material to the Bibliotheque Nationale. Two days ago, Le Monde wrote that the legacy consists of some 50.000 pages.
Maltsiniotis insisted that the BNF wants to make these notes available to the academic community, after they made an inventory (which may take some time).
I guess from the blackboard-picture i got from Pieter, the person responsible at the BNF is Isabelle le Masme de Chermont.
The Lasserre-griboillis themselves consists of 5 parts:
1. Géométrie élémentaire schématique. (August 1992)
This is about quadratic forms and seems to be really elementary.
2. Structure de la psyché. (12/10/1992-28/09/1993) 3600 pages
This one is about some combinatorics of oriented graphs with extra-structure (part of the structure are successor and predecessor operators on the set of arrows).
3. Psyché et structures (26/03/93-20/06/93) 700 pages
This one is non-mathematical.
4. Maxwell equations.
Maltsiniotis mentioned that he was surprised to see that there was at best one mathematics book in G’s home, but plenty of physics books.
5. Le problème du mal. (1993-1998)
This one is huge (30.000 pages) and is non-mathematical.
Note that also the Mormoiron-gribouillis will be made public by the University of Montpellier, or if you prefer video.
Finally, is the photo below what you think it is? Yep!

January 20th, 2016
where are the videos of the Grothendieck conference?
Mid june 2015 a conference “Mathematics of the 21st century: the vision of Alexander Grothendieck” was held in Montpellier. In a comment to a post here on Maltsiniotis’ talk i mentioned that most of the talks were video-taped and that they would soon be made public.
When they failed to surface on the Montpellier website, i asked +Damien Calaque for more information. Some months ago Damien told me the strange (and worrying) tale of their fate.
At that moment Damien was in a process of trying to recover the videos. Two weeks ago he told me things were looking good, so i now feel free to post about it.
Michael Wright is the head of the Archive for Mathematical Sciences & Philosophy. He arranged with the organizers of the conference that he would send someone over to video-tape the lectures and that he would make them available on his Archive. He also promised to send a copy of the videos to Montpellier, but he never did. Nor did the tapes appear on his site.
Damien Calague emailed Wright asking for more information and eventually got a reply. It appears that Wright will not be able to edit the videos nor put them online in a reasonable time.
They agreed that Damien would send him a large capacity USB-drive. Wright would copy the videos on it and send it back. Damien will arrange for the videos to be edited and the University of Montpellier will put them online. Hopefully everything will work out smoothly.
So please keep an eye on the website of l’Institut Montpelliérain Alexander Grothendieck

May 6th, 2017
Grothendieck’s Montpellier notes will hit the net May 10th
At last there is an agreement between the university at Montpellier and Grothendieck’s children to release the ‘Montpellier gribouillis’ (about 28000 pages will hit the net soon).
Another 65000 pages, found at Lasserre after Grothendieck’s death, might one day end up at the IHES or the Bibliotheque Nationale.
If you are interested in the history of Grothendieck’s notes, there is this old post on my blog.
(h/t Theo Raedschelders for the Liberation link)
May 11th, 2017
Buy a Grothendieck painting to get the Lasserre notes online!
As of yesterday, most of Grothendieck’s Montpellier notes are freely available at this site.
There’s much to say about the presentation (eg. It is not possible to link directly to a given page/article, it is scanned at only 400 dpi etc. etc.) but hey, here they are at last, for everyone to study.
By far the most colourful (in my first browsing of the archive) is cote No. 154, on ‘systeme de pseudo-droites’. You can download it in full (a mere 173 Mb).
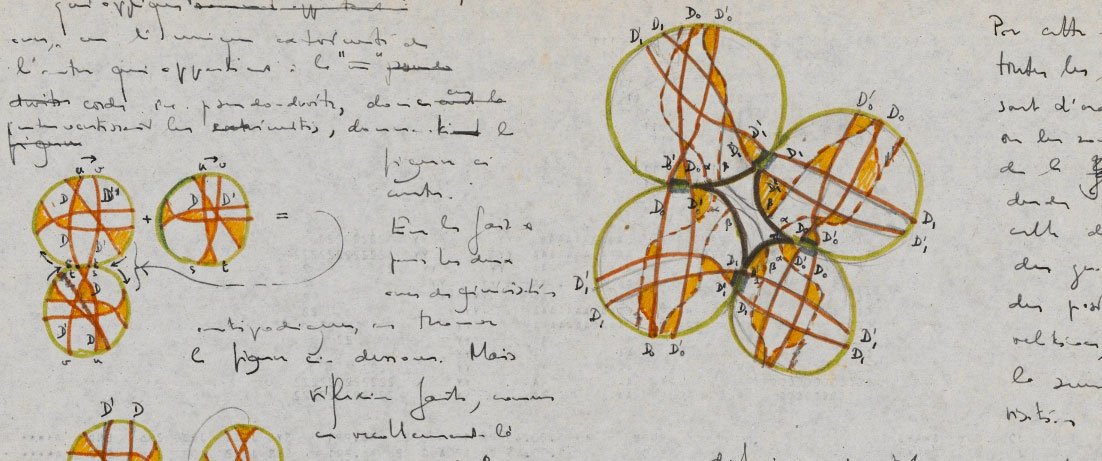
As you know, the Montpellier notes are only a fraction of the material Grothendieck left behind. By far the largest (though probably not the most interesting, mathematically) are the Lasserre notes, which to the best of my knowledge are in the care of a Parisian bookseller.
Here’s an idea:
almost every page of No. 154 (written on ancient computer-output) looks like a painting. No doubt, most math departments in the world would love to acquire one framed page of it. Perhaps this can raise enough money to safeguard the Lasserre notes…
July 13th, 2017
le Tour de France in Grothendieck’s backyard
If you want to see the scenery Grothendieck enjoyed in his later years, watch the Tour de France tomorrow.
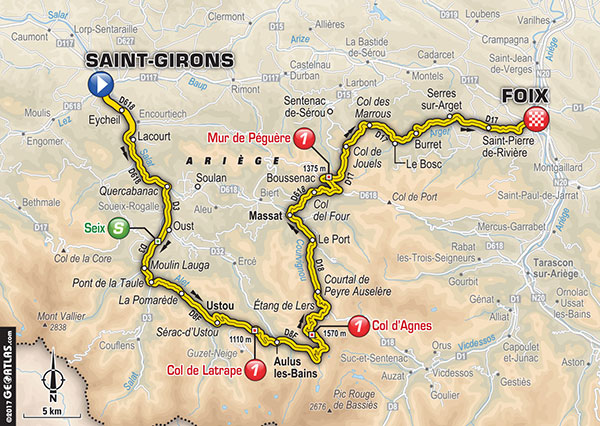
It starts in Saint-Girons where he went to the weekly market (and died in hospital, november 13th 2014), ending in Foix with 3 category 1 climbs along the way (familiar to anyone familiar with Julia Stagg’s expat-lit set at ‘Fogas’ or you can read my own post on Fogas).
It will not pass through Lasserre (where G spend the final 20 years of his life) which is just to the north of Saint-Girons.
One Comment

