Who was the first mathematician to give a slide show talk? I don’t have the
definite answer to this question, but would like to offer a strong
candidate :  Hermann Minkowski gave the talk “Zur Geometrie der Zahlen” (On the
Hermann Minkowski gave the talk “Zur Geometrie der Zahlen” (On the
geometry of numbers) before the third ICM in 1904 in Heidelberg and even
the title page of his paper in the proceedings indicates that he did
present his talk using slides (Mit Projektionsbildern auf einer
Doppeltafel)

Seven
of these eight slides would be hard to improve using LaTeX
 What concerns
What concerns
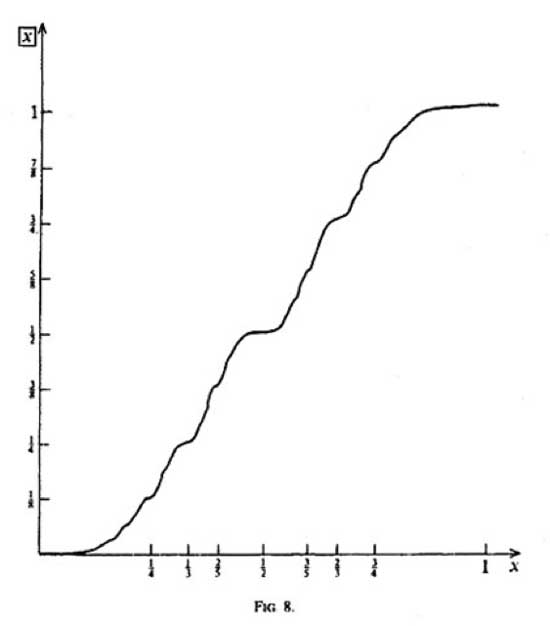
us today is the worst of all slides, the seventh, where Minkowski tries
to depict his famous questionmark function $?(x) $, sometimes also called
the _devil’s staircase_
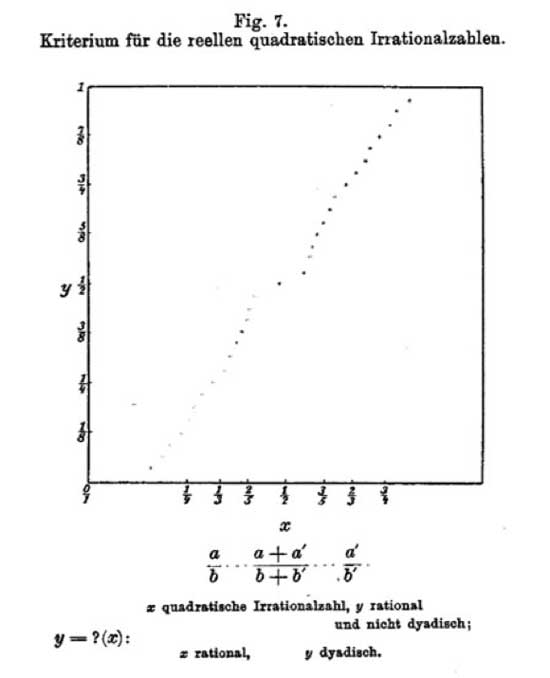
The devil’s
staircase is a fractal curve and can be viewed as a mirror (taking a
point on the horizontal axis to the point on the vertical axis through
the function value) having magical simplifying properties : – it takes
rational numbers to _dyadic numbers_, that is those of the form
$n.2^{-m}$ with $n,m \in \mathbb{Z} $. – it takes quadratic
_irrational_ numbers to rational numbers. So, iterating this
mirror-procedure, the devil’s staircase is a device solving the main
problem of Greek Mathematics : which lengths can be constructed using
ruler and compass? These _constructible numbers_ are precisely those
real numbers which become after a finite number of devil-mirrors a
dyadic number. The proofs of these facts are not very difficult but
they involve a piece of long-forgotten mathematical technology :
_continued fractions_. By repeted approximations using the
floor-function (the largest natural number less than or equal to the real
number), every positive real number can be written as
$a = a_0 +
\frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \frac{1}{\dots}}}} $
with all $a_i $ natural numbers. So, let us just denote from now on this
continued fraction of a by the expression
$a = \langle
a_0;a_1,a_2,a_3,\dots \rangle $
Clearly, a is a rational number if
(and also if but this requires a small argument using the Euclidian
algorithm) the above description has a tail of zeroes at the end and
(slightly more difficult) $a$ is a real quadratic irrational number
(that is, an element of a quadratic extension field
$\mathbb{Q}\sqrt{n} $) if and only if the continued fraction-expression
has a periodic tail. There is a lot more to say about
continued-fraction expressions and I’ll do that in another
‘virtual-course-post’ (those prepended with a (c): sign). For the
impatient let me just say that two real numbers will lie in the same
$GL_2(\mathbb{Z}) $-orbit (under the action via Moebius-transformations)
if and only if their continued fraction expressions have the same tails
eventually (which has applications in noncommutative geometry as in the
work of Manin and Marcolli but maybe I’ll come to this in the (c):
posts).
Right, now we can define the mysterious devil-stair function
$?(x) $. If a is in the real interval $[0,1] $ and if $a \in
\mathbb{Q} $ then $a = \langle 0;a_1,a_2,\dots,a_n,0,0,\dots
\rangle $ and we define $?(a) = 2 \sum_{k=1}^{n} (-1)^k
2^{-(a_1+a_2+\dots+a_k)} $ and if a is irrational with continued
fraction expression $a = \langle 0;a_1,a_2,a_3,\dots \rangle $, then
$?(a) = 2 \sum_{k=1}^{\infty} (-1)^{k+1} 2^{-(a_1+a_2+\dots+a_k)} $
A
perhaps easier description is that with the above continued-fraction
expression, the _binary_ expansion of $?(a) $ has the following form
$?(a) = 0,0 \dots 01 \dots 1 0 \dots 0 1 \dots 1 0 \dots 0 1 \dots
1 0 \dots $
where the first batch of zeroes after the comma has length
$a_1-1 $, the first batch of ones has length $a_2 $ the next batch of
zeroes length $a_3 $ and so on.
It is a pleasant exercise to verify that
this function does indeed have the properties we claimed before. A
recent incarnation of the question mark function is in Conway’s game of
_contorted fractions_. A typical position consists of a finite number of
boxed real numbers, for example the position might be
$\boxed{\pi} + \boxed{\sqrt{2}} + \boxed{1728} +
\boxed{-\frac{1}{3}} $
The Rules of the game are : (1) Both
players L and R take turns modifying just one of the numbers such that
the denominator becomes strictly smaller (irrational numbers are
supposed to have $\infty$ as their ‘denominator’). And if the boxed
number is already an integer, then its absolute value must decrease.
(2) Left must always _decrease_ the value of the boxed number, Right
must always increase it. (3) The first player unable to move looses
the game. To decide who wins a particular game, one needs to compute
the value of a position $\boxed{x} $ according to the rules of
combinatorial game theory (see for example the marvelous series of four
books Winning Ways for your Mathematical Plays. It turns out that this CG-value is no other than $?(x)$
… And, Conway has a much improved depiction of the devil-staircase in
his book On Numbers And Games