Suppose for a moment that some librarian at the Bodleian Library announces that (s)he discovered an old encrypted book attributed to Isaac Newton. After a few months of failed attempts, the code is finally cracked and turns out to use a Public Key system based on the product of two gigantic prime numbers, $2^{32582657}-1 $ and $2^{30402457}-1 $, which were only discovered to be prime recently. Would one deduce from this that Newton invented public key cryptography and that he used alchemy to factor integers? (( Come to think of it, some probably would ))
The cynic in me would argue that it is a hell of a coincidence for this text to surface exactly at the moment in history when we are able to show these numbers to be prime and understand their cryptographic use, and conclude that the book is likely to be a fabrication. Still, stranger things have happened in the history of mathematics…
 In 1773, Gotthold Ephraim Lessing at that time librarian at the Herzog-August-Bibliothek discovered and published a Greek epigram in 22 elegiac couplets. The manuscript describes a problem sent by Archimedes to the mathematicians in Alexandria.
In 1773, Gotthold Ephraim Lessing at that time librarian at the Herzog-August-Bibliothek discovered and published a Greek epigram in 22 elegiac couplets. The manuscript describes a problem sent by Archimedes to the mathematicians in Alexandria.
In his beautiful book “Number Theory, an approach through history. From Hammurapi to Legendre” Andre Weil asserts (( Chapter I,IX )):
Many mathematical epigrams are known. Most of them state problems of little depth; not so Lessing’s find; there is indeed every reason to accept the attribution to Archimedes, and none for putting it into doubt.
This Problema Bovidum (the cattle problem) is a surprisingly difficult diophantine problem and the simplest complete solution consists of eigth numbers, each having about 206545 digits. As we will see later the final ingredient in the solution is the solution of Pell’s equation using continued fractions discovered by Lagrange in 1768 and published in 1769 in a long memoir. Lagrange’s solution to the Pell equation was inserted in Euler’s “Algebra” which was composed in 1771 but published only in 1773… the very same year as Lessing’s discovery! (( all dates learned from Weil’s book Chp. III,XII ))
Weil’s book doesn’t include the details of the original epigram. The (lost) archeologist in me wanted to see the original Greek 22 couplets as well as a translation. So here they are : (( thanks to the Cattle problem site ))
 A PROBLEM
A PROBLEM
which Archimedes solved in epigrams, and which he communicated to students of such matters at Alexandria in a letter to Eratosthenes of Cyrene.
If thou art diligent and wise, O stranger, compute the number of cattle of the Sun, who once upon a time grazed on the fields of the Thrinacian isle of Sicily, divided into four herds of different colours, one milk white, another a glossy black, a third yellow and the last dappled. In each herd were bulls, mighty in number according to these proportions: Understand, stranger, that the white bulls were equal to a half and a third of the black together with the whole of the yellow, while the black were equal to the fourth part of the dappled and a fifth, together with, once more, the whole of the yellow. Observe further that the remaining bulls, the dappled, were equal to a sixth part of the white and a seventh, together with all of the yellow. These were the proportions of the cows: The white were precisely equal to the third part and a fourth of the whole herd of the black; while the black were equal to the fourth part once more of the dappled and with it a fifth part, when all, including the bulls, went to pasture together. Now the dappled in four parts were equal in number to a fifth part and a sixth of the yellow herd. Finally the yellow were in number equal to a sixth part and a seventh of the white herd. If thou canst accurately tell, O stranger, the number of cattle of the Sun, giving separately the number of well-fed bulls and again the number of females according to each colour, thou wouldst not be called unskilled or ignorant of numbers, but not yet shalt thou be numbered among the wise.
But come, understand also all these conditions regarding the cattle of the Sun. When the white bulls mingled their number with the black, they stood firm, equal in depth and breadth, and the plains of Thrinacia, stretching far in all ways, were filled with their multitude. Again, when the yellow and the dappled bulls were gathered into one herd they stood in such a manner that their number, beginning from one, grew slowly greater till it completed a triangular figure, there being no bulls of other colours in their midst nor none of them lacking. If thou art able, O stranger, to find out all these things and gather them together in your mind, giving all the relations, thou shalt depart crowned with glory and knowing that thou hast been adjudged perfect in this species of wisdom.
The Lessing epigram may very well be an extremely laborious hoax but it is still worth spending a couple of posts on it. It gives us the opportunity to retell the amazing history of Pell’s problem rangingfrom the ancient Greeks and Indians, over Fermat and his correspondents, to Euler and Lagrange (with a couple of recent heroes entering the story). And, on top of this, the modular group is all the time just around the corner…
4 Comments Farey sequences have plenty of mysterious properties. For example, in 1924 J. Franel and
Farey sequences have plenty of mysterious properties. For example, in 1924 J. Franel and 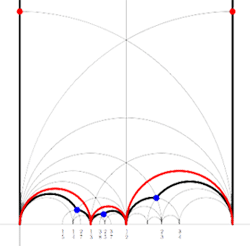 Recall from
Recall from 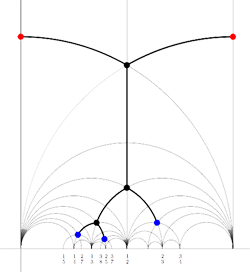
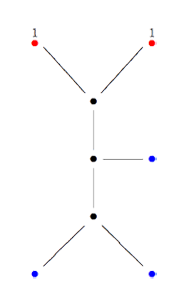
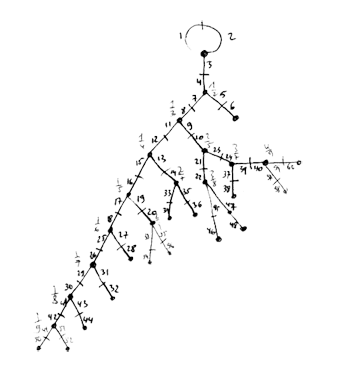
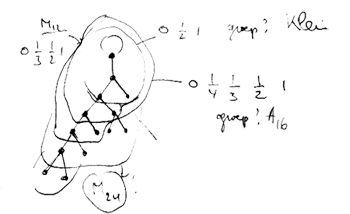
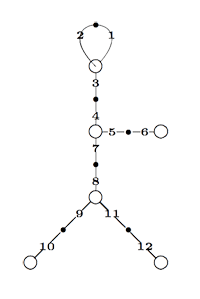 Finally, identifying the red points (as they lie on geodesics connected to $\infty $ which are identified in the Farey code), adding even points on the remaining geodesics and numbering the obtained half-lines we obtain the dessin d’enfant given on the left hand side. To such a dessin we can associate its monodromy group which is a permutation group on the half-lines generated by an order two element indicating which half-lines make up a line and an order three element indicating which half-lines one encounters by walking counter-clockwise around a three-valent vertex. For the dessin on the left the group is therefore the subgroup of $S_{12} $ generated by the elements
Finally, identifying the red points (as they lie on geodesics connected to $\infty $ which are identified in the Farey code), adding even points on the remaining geodesics and numbering the obtained half-lines we obtain the dessin d’enfant given on the left hand side. To such a dessin we can associate its monodromy group which is a permutation group on the half-lines generated by an order two element indicating which half-lines make up a line and an order three element indicating which half-lines one encounters by walking counter-clockwise around a three-valent vertex. For the dessin on the left the group is therefore the subgroup of $S_{12} $ generated by the elements