Skip to content →

neverendingbooks Posts

SMS-Math Meme (SMM)

Published December 21, 2007 by lievenlb

Hey, here’s an idea : The Text-Math Book! Trying to promote mathematics while at the same time acknowledging the fairly limited attention-span of the intended generation, let’s try to write a book on serious maths following just one rule

EVERY DEFINITION, THEOREM AND PROOF IN THE BOOK SHOULD NOT BE LONGER THAN A TEXT-MESSAGE (ie. 160 chars)

I don’t even own a cell phone (( waiting for the iPhone to arrive in Belgium )), so PLEASE educate me youngsters! SMS your contribution, either as a comment left here or hosted at your own blog (please link, so that I can learn…, a full text explanation of abbreviations used will be applauded.)

2 Comments

Wiki on iTouch

Published December 20, 2007 by lievenlb

I’ve reduced the springboard of my jailbroken iTouch to a minimalistic Dock consisting only of the iPhone Mail.app to read and write mails properly (as opposed to having to use webmail on an unbroken iTouch), an RSS-reader to watch other math-blogs and the arXiv (via Install.app under Productivity/MobileRSS), the Safari webbrowser and a Finder (via Install.app under Productivity/MobileFinder) to launch all other programs, when needed.

To achieve this effect, install (as in the jailbreak-post) all these apps as well as Customize.app (under Utilities). This allows you to change the icon order on your springboard and dock as well as to toggle the visibility of these icons. Just make sure to have either Finder or Customize visible at all times or it will be difficult to get at the invisible apps (an alternative is to install something called Sunburst).

While the iTouch is great to read, it is harder to type a lot of text into it. Whence the idea of running a Wiki on it (now that we have PHP enabled Apache) and use another computer to create the wiki-pages. For example think of a small database of weblinks with descriptions. Rather than bookmark them one by one in Safari, make wiki-pages for them and use the Search function to get the desired link.

The first problem is that Wikis take a lot of space and you would like to have it installed under /Library/WebServer/Documents to view it with your inbuild Safari browser by typing something like http://localhost/wiki. To see the problem with this, ssh into your iTouch and issue a df command. You will get something like

# df
Filesystem           1K-blocks      Used Available Use% Mounted on
/dev/disk0s1            307200    297188      6940  98% /
devfs                       15        15         0 100% /dev
/dev/disk0s2          15551928    517904  15034024   4% /private/var

That is, you’ve used up almost all disk space of the partition on which the /Library/WebServer/Documents folder resides. So, we first need to move it to the other partition under /private/var, so why not create a Documents-folder under the root-homefolder and link to it?

cd /Library/WebServer
mv Documents /private/var/root/
ln -s /private/var/root/Documents Documents

Check it with http://localhost/ and you should still see your default Apache-page (though it now comes from another location). The next step is to find a PHP-Wiki hat works on the iTouch and doesn’t require a Mysql-database. I’ve tried at least ten without success and then I turned to the Wiki Engines Page and found QWikiWiki which does seem to work. So download it, rename the folder to something you like such as ‘qwiki’ and upload via SFTP to the /var/root/Documents folder of your iTouch and chmod it recursively to 777. If you ever need to change some of the PHP-variables, copy the php.ini from you mac over to the /opt/iphone/bin folder of the iTouch.

Finally, use a browser on your other computer to access the install file of Qwiki on the iTouch. For example, if the IP of iTouch is 10.0.1.197 then type

http://10.0.1.197/qwiki/install.php

and follow the online instructions. A few moments later you can type in your first wiki-page!

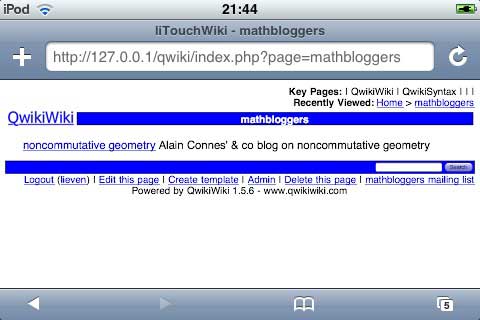
Some things still need to be done like optimizing the CSS for iTouch while serving the normal CSS for usual computers, but that’ll have to wait…

4 Comments

Anabelian & Noncommutative Geometry 2

Published December 19, 2007 by lievenlb

Last time (possibly with help from the survival guide) we have seen that the universal map from the modular group $\Gamma = PSL_2(\mathbb{Z}) $ to its profinite completion $\hat{\Gamma} = \underset{\leftarrow}{lim}~PSL_2(\mathbb{Z})/N $ (limit over all finite index normal subgroups $N $) gives an embedding of the sets of (continuous) simple finite dimensional representations

$\mathbf{simp}_c~\hat{\Gamma} \subset \mathbf{simp}~\Gamma $

and based on the example $\mu_{\infty} = \mathbf{simp}_c~\hat{\mathbb{Z}} \subset \mathbf{simp}~\mathbb{Z} = \mathbb{C}^{\ast} $ we would like the above embedding to be dense in some kind of noncommutative analogon of the Zariski topology on $\mathbf{simp}~\Gamma $.

We use the Zariski topology on $\mathbf{simp}~\mathbb{C} \Gamma $ as in these two M-geometry posts (( already, I regret terminology, I should have just called it noncommutative geometry )). So, what’s this idea in this special case? Let $\mathfrak{g} $ be the vectorspace with basis the conjugacy classes of elements of $\Gamma $ (that is, the space of class functions). As explained here it is a consequence of the Artin-Procesi theorem that the linear functions $\mathfrak{g}^{\ast} $ separate finite dimensional (semi)simple representations of $\Gamma $. That is we have an embedding

$\mathbf{simp}~\Gamma \subset \mathfrak{g}^{\ast} $

and we can define closed subsets of $\mathbf{simp}~\Gamma $ as subsets of simple representations on which a set of class-functions vanish. With this definition of Zariski topology it is immediately clear that the image of $\mathbf{simp}_c~\hat{\Gamma} $ is dense. For, suppose it would be contained in a proper closed subset then there would be a class-function vanishing on all simples of $\hat{\Gamma} $ so, in particular, there should be a bound on the number of simples of finite quotients $\Gamma/N $ which clearly is not the case (just look at the quotients $PSL_2(\mathbb{F}_p) $).

But then, the same holds if we replace ‘simples of $\hat{\Gamma} $’ by ‘simple components of permutation representations of $\Gamma $’. This is the importance of Farey symbols to the representation problem of the modular group. They give us a manageable subset of simples which is nevertheless dense in the whole space. To utilize this a natural idea might be to ask what such a permutation representation can see of the modular group, or in geometric terms, what the tangent space is to $\mathbf{simp}~\Gamma $ in a permutation representation (( more precisely, in the ‘cluster’ of points making up the simple components of the representation representation )). We will call this the modular content of the permutation representation and to understand it we will have to compute the tangent quiver $\vec{t}~\mathbb{C} \Gamma $.

Leave a Comment