This semester, I’m running a 3rd year course on Marcus du Sautoy’s The music of the primes. The concept being that students may suggest topics, merely sketched in the book, and then we’ll go a little deeper into them.
I’ve been rather critical about the book before, but, rereading it last week (and knowing a bit better the limitations of bringing mathematics to the masses…) I think du Sautoy did a great job. Sure, it focusses too much on people and places and too little on mathematics, but that goes with the format.
I wanted to start off gently by playing the open-university dvd-series so that students would have a very rough outline of the book from the very start (as well as a mental image to some of the places mentioned, such as Bletchley Park, the IAS, Gottingen…). However, the vagueness of it all seemed to work on their nerves … in particular the trumpet scenes

Afterwards, they demanded that I should explain next week what on earth the zeroes of the Riemann zeta function had to do with counting primes and what all this nonsensical ‘music of the primes’ was about.
Well, here is the genuine music of the primes (taken from the Riemann page by Jeffrey Stopple whose excellent introductory text A Primer of Analytic Number Theory I’ll use to show them some concrete stuff (they have their first course on complex analysis also this semester, so I cannot go too deep into it).
Jeffrey writes “This sound is best listened to with headphones or external speakers. For maximum effect, play it LOUD.” But, what is the story behind it?
The Von Mangoldt function $\Lambda(n) $ assigns $log(p) $ whenever $n=p^k $ is a prime power and zero otherwise. One can then consider the function
$\Psi(x) = \frac{1}{2}(\sum_{n < x} \Lambda(n) + \sum_{n \leq x} \Lambda(n)) $
which makes a jump at prime power values and the jump-size depends on the prime. Here is a graph of its small values
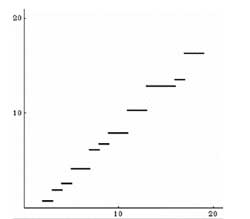 It’s not quite the function $\pi(x) $ (counting the number of primes smaller than x) but it sure contains enough information to obtain this provided we have a way of describing $\Psi(x) $.
It’s not quite the function $\pi(x) $ (counting the number of primes smaller than x) but it sure contains enough information to obtain this provided we have a way of describing $\Psi(x) $.
The Riemann zeta function (or rather $~(s-1)\zeta(s) $) has two product descriptions, the Hadamard product formula (running over all zeroes, both the trivial ones at $-2n $ and those in the critical strip), which is valid for all complex s and the Euler product valid for all $Re(s) > 1 $. This will allow us to calculate in two different ways $\zeta'(s)/\zeta(s) $ which in turn allows us to have an explicit description of $\Psi(s) $ known as the Von Mangoldt formula
$\Psi(x) = x – \frac{1}{2}log(1 – \frac{1}{x^2}) – log(2 \pi) – \sum_{\rho} \frac{x^{\rho}}{\rho} $
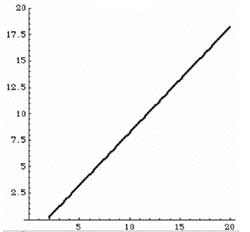
where only the last term depends on the zeta-zeroes $\rho $ lying in the critical strip (and conjecturally all lying on the line $Re(x) = \frac{1}{2} $. The first few terms (those independent of the zeroes) give a continuous approximation of $\Psi(x) $ but how on earth can we get from that approxamation (on the left) to the step-like function itself (on the right)?

We can group together zeta-zeroes $\rho=\beta + i \gamma $ with their comlex conjugate zeroes $\overline{\rho} $ and then one shows that the attribution to the Von Mangoldt formula is
$\frac{x^{\rho}}{\rho} + \frac{x^{\overline{\rho}}}{\overline{rho}} = \frac{2 x^{\beta}}{| \rho | }cos(\gamma log(x) – arctan(\gamma/\beta)) $
Ignoring the term $x^{\beta} $ this is a peridodic function with amplitude $2/| \rho | $ (so getting smaller for larger and larger zeroes) and period $2\pi/ \gamma $. If the Riemann hypothesis holds (meaning that $\beta=1/2 $ for all zeroes) one can even split a term in this contribution of every zero as a sort of ‘universal amplitude’. What is left is then a sum of purely periodic functions which a physicist will view as a superposition of (sound) waves and that is the music played by the primes!
Below, a video of the influence of adding the first 100 zeroes to a better and better approximation of $\Psi(x) $ (again taken from the Riemann page by Jeffrey Stopple). Surely watching the video will convince anyone of the importance of the Riemann zeta-zeroes to the prime-counting problem..