 Via the Arcadian functor I learned of the existence of the Sudokube (picture on the left).
Via the Arcadian functor I learned of the existence of the Sudokube (picture on the left).
Sudokube is a variation on a Rubik’s Cube in which each face resembles one-ninth of a Sudoku grid: the numbers from one to nine. This makes solving the cube slightly more difficult than a conventional Rubik’s Cube because each number must be in the right place and the centre cubies must also be in the correct orientation.
A much more interesting Sudoku-variation of the cube was invented two weeks ago by one of my freshmen-grouptheory students and was dubbed the mini-sudokube by him. Here’s the story.
At the end of my grouptheory course I let the students write a paper to check whether they have research potential. This year the assignment was to read through the paper mini-sudokus and groups by Carlos Arcos, Gary Brookfield and Mike Krebs, and do something original with it.
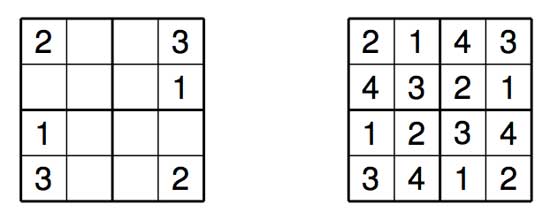
Mini-Sudoku is the baby $2 \times 2 $ version of Sudoku. Below a trivial problem and its solution
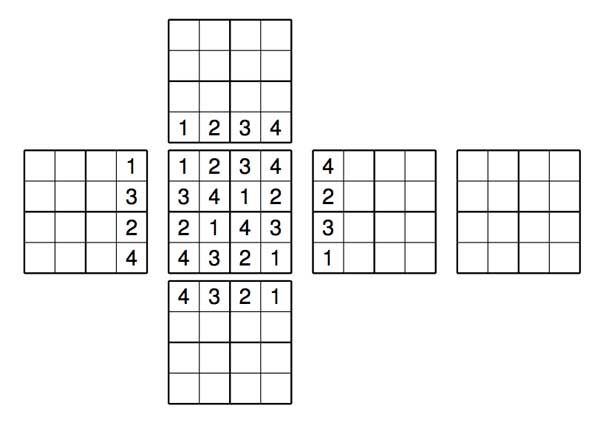
Of course most of them took the safe road and explained in more detail a result of the paper. Two of them were more original. One used the mini-sudoku solutions to find solutions for 4×4 sudokus, but the most original contribution came from Ibrahim Belkadi who wanted to count all mini-sudokubes. A mini-sudokube is a cube with a mini-sudoku solution on all 6 of its sides BUT NUMBERS CARRY OVER CUBE-EDGES. That is, if we have as the mini-sudoku given by the central square below on the top-face of the cube, then on the 4 side-faces we have already one row filled in.
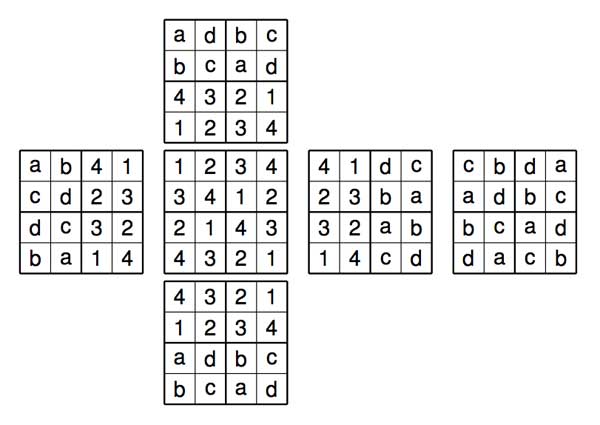
The problem then is to find out how many compatible solutions there are. It is pretty easy to see that top- and bottom-faces determine all squares of the cube, but clearly not all choices are permitted. For example, with the above top-face fixed there are exactly 4 solutions. Let ${ a,b } = { 1,4 } $ and ${ c,d } = { 2,3 } $ then these four solutions are given below
Putting one of these solutions (or any other) on a $4 \times 4 $-Rubik cube would make a more interesting puzzle, I think. I’ve excused Ibrahim from having to take examination on condition that he writes down what he can prove on his mini-sudokubes by that time. Looking forward to it!
One Comment