Conway’s orbifold notation gives a uniform notation for all discrete groups of isometries of the sphere, the Euclidian plane as well as the hyperbolic plane.
This includes the groups of symmetries of Escher’s Circle Limit drawings. Here’s Circle Limit III

And ‘Angels and Devils’ aka Circle Limit IV:

If one crawls along a mirror of this pattern until one hits another mirror and then turns right along this mirror and continues like this, you get a quadrilateral path with four corners $\frac{\pi}{3}$, whose center seems to be a $4$-fold gyration point. So, it appears to have symmetry $4 \ast 3$.
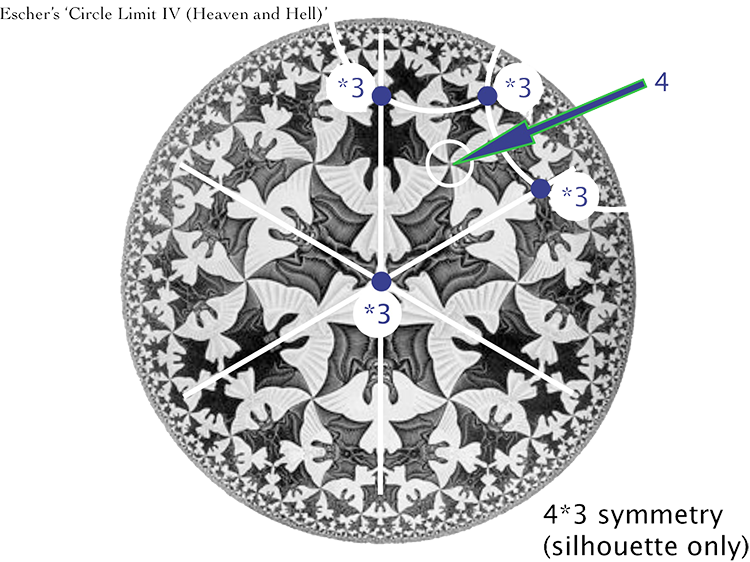
(image credit: MathCryst)
However, looking more closely, every fourth figure (either devil or angel) is facing away rather than towards us, so there’s no gyration point, and the group drops to $\ast 3333$.
Harold S. M. Coxeter met Escher in Amsterdam at the ICM 1954.
The interaction between the two led to Escher’s construction of the Circle Limits, see How did Escher do it?
Here’s an old lecture by Coxeter on the symmetry of the Circle Limits:
Comments