Category: tBC

Where’s Bourbaki’s tomb?

Published October 23, 2016 by lievenlb

In according to Groth IV.22 we tried to solve one of the riddles contained in Roubaud’s announcement of Bourbaki’s death.

Today, we’ll try our hands on the next one: where was Bourbaki buried?

The death announcement gives this fairly opaque clue:

“The burial will take place in the cemetery for Random Functions (metro stations Markov and Gödel) on Saturday, November 23, 1968 at 3 o’clock in the afternoon.”

What happened on November 23rd 1968?

Bourbaki died on November 11th, 1968 (exactly 50 years after the end of WW1). Perhaps an allusion to the mandatory retirement age for members of Bourbaki, as suggested by the Canulars Bourbaki.

Be that as it may, I believe this date was chosen because it is conveniently close to the intended time of the burial.

But then, what’s so special about November 23rd, 1968?

Well, is there a more suitable moment to burry Bourbaki than during a Seminaire Bourbaki? And, yes, in the fall of 1968 the seminar was organised from saturday 23rd till monday 25th of november:

So, where would all of Bourbaki’s close family be at 3 o’clock on that particular saturday? Right, at l’Institut Henri Poincare.

But, it’s hard to view the IHP as a cemetery. Besides, it’s nowhere close to two metro stations as a quick look on the map shows. The closest one is the RER-station at the Luxembourg gardens, but the RER-line didn’t exist in 1968.

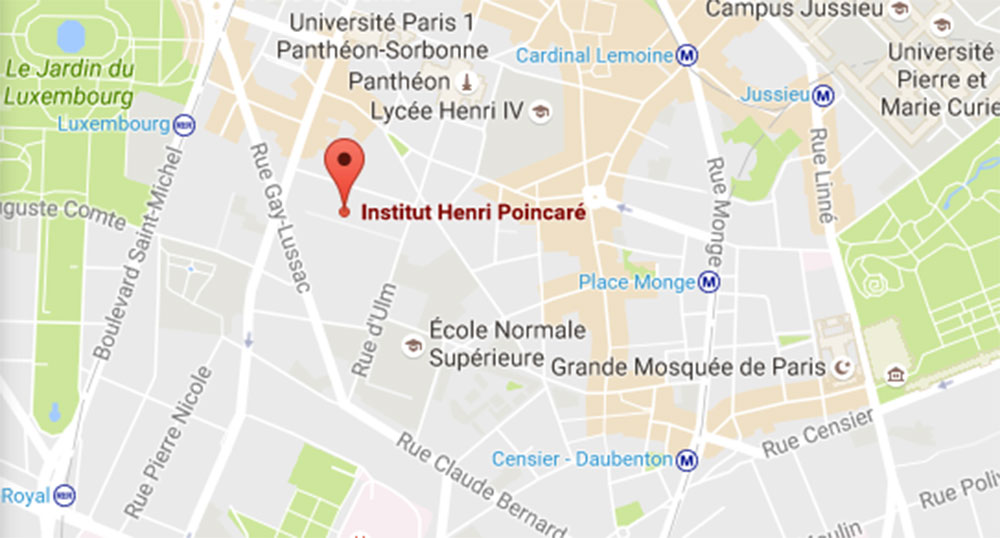
(True Parisians may object that the Gare du Luxembourg was at the time the terminus of the Ligne de Sceaux which has a fascinating history, but let’s try to remain on track…)

If the first clue is the Institut Henri Poincare, then if we are looking for a cemetery, we might ask:

Where’s Poincare’s tomb?

Jules Henri Poincare is burried in the family tomb at the Montparnasse cemetery

He’s not the only mathematician buried there. Évariste Galois, Jean Victor Poncelet, Joseph Liouville, Charles Hermite, and Gaston Darboux also found their last resting place in Montparnasse.

In fact, there are at least 104 mathematicians buried at Montparnasse.

This is hardly surprising as the Montparnasse cemetery is close to the IHP, the Collège de France, the Sorbonne, the “rue d’Ulm” aka the ENS, l’Observatoire and until 1976 l’École polytechnique.

Here’s a map with pointers to some of these tombs:

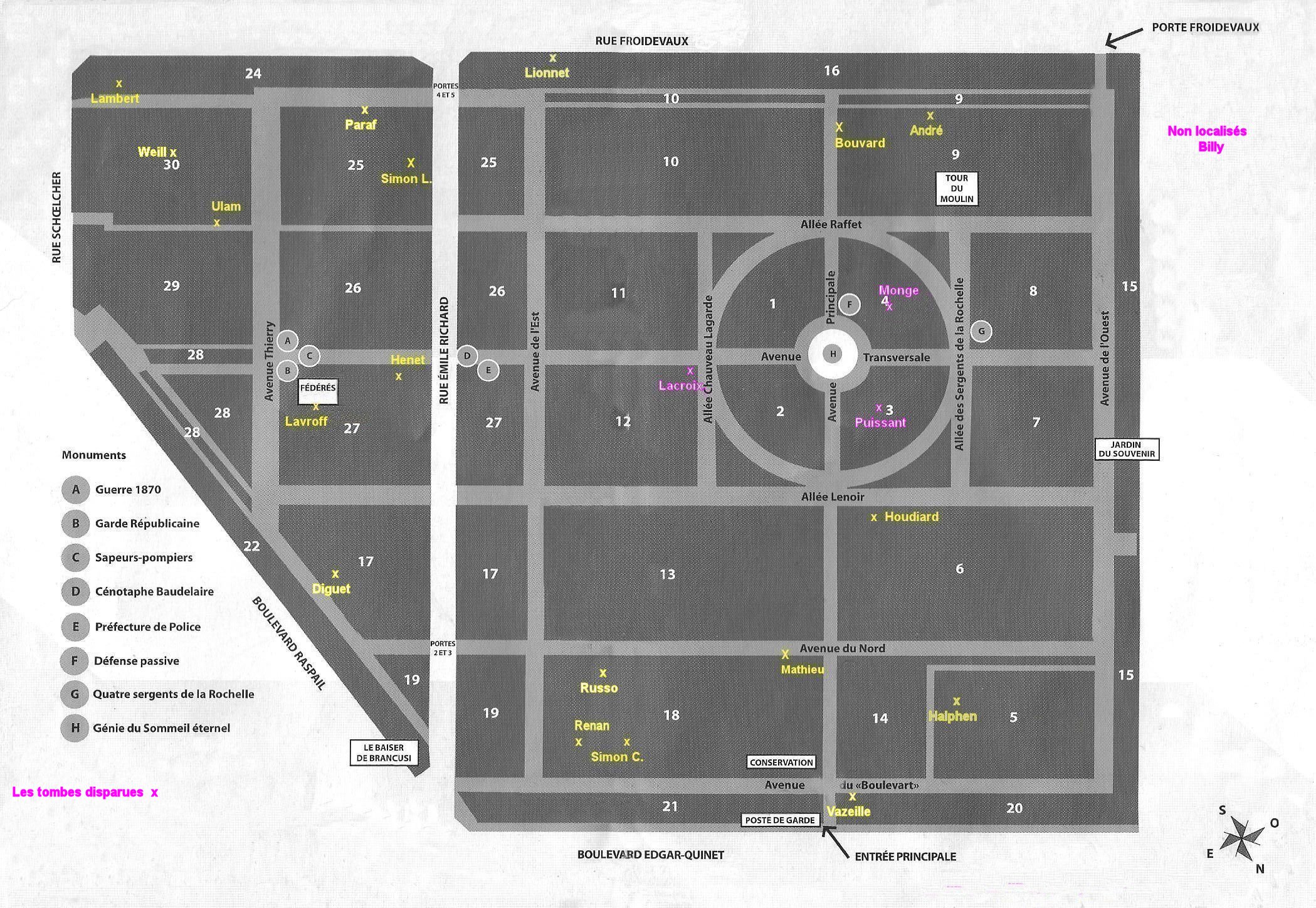
So, the Montparnasse cemetery appears to be a plausible place to host Bourbaki’s tomb.

But, what about the other “clues”?

“Cemetery of random functions (metro stations Markov and Gödel)”

There are several references lo logic, set theory and applied mathematics in Bourbaki’s death announcement. Why?

Roubaud (and many with him) feel that the Bourbaki enterprise failed miserably in these areas.

He writes on page 49 of his book Mathematics, a novel:

“But Bourbaki, that ‘collective mathematician”, as Raymond Queneau put it, also had a good knowledge of the current state of mathematics at the time when his Treatise was being composed; with, of course, a few “gaps”:

for example, probability, which was considered to be just an “applied” brand of measure theory”; and logic, especially logic, which was made almost a pariah because of (so it was rumored) the premature death of Herbrand, who, in the generation of founders, Normaliens to a man, had studied under Hilbert, and thus had been associated with his meteoric rise; in sum, logic had died in a climbing accident along with Herbrand.”

This might explain the cemetery of “random functions” and the metro stations named after the logicians and set theorists Kurt Gödel and A.A. Markov or the father of stochastic processes Andrey Markov.

Is there more into these references?

Probably not, but just to continue with our silly game, the two metro stations closest to the Montparnasse cemetery are Raspail and Edgar Quinet.

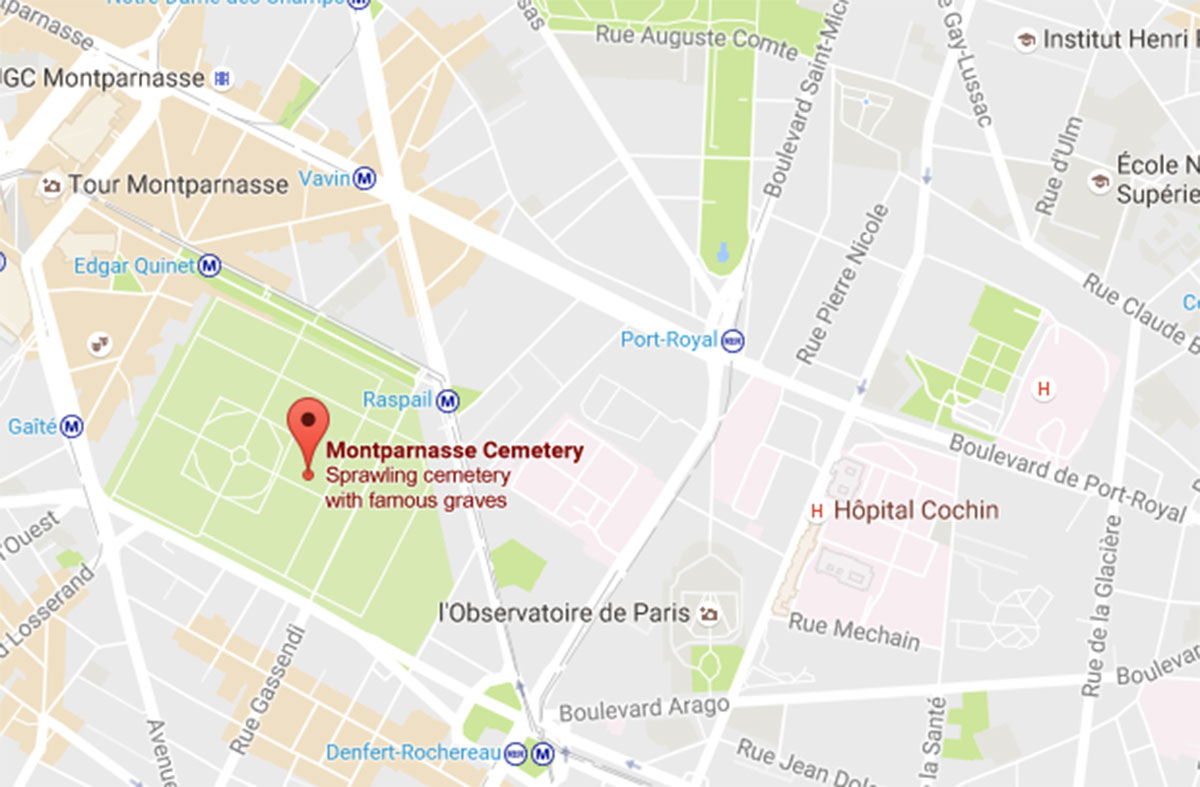
Now, François-Vincent Raspail was a French chemist, naturalist, physician, physiologist, attorney, and socialist politician.

More relevant to our quest is that the Centre d’analyse et de mathématique sociales (CAMS) was based at 54, boulevard Raspail. The mission statement on their website tells that this institute is clearly devoted to all applications of mathematics. That is, “Raspail” may be another pointer to applied mathematics and random functions.

As for the other metro station, Edgar Quinet was a French historian and intellectual. Is there a connection to logic or set theory? Well, sort of. The Encyclopedia Britannica has this to say about Edgar Quinet:

“His rhetorical power was altogether superior to his logical power, and the natural consequence is that his work is full of contradictions.”

I rest my case.

Hasse = “le P. Adique, de l’Ordre des Diophantiens”

Published October 12, 2016 by lievenlb

The Bourbaki wedding invitation is probably the most effective branding- and marketing-campaign in the history of mathematics.

It contains this, seemingly opaque, paragraph:

The trivial isomorphism will be given to them by P. Adic, of the Diophantine Order, at the Principal Cohomology of the Universal Variety, the 3 Cartember, year VI, at the usual hour.

It was pretty easy to decode the date of the wedding “3 Cartember, year VI” to be June 3rd, 1939, and (a bit more difficult) the wedding place “the Principal Cohomology of the Universal Variety” as the l’église royale Notre-Dame du Val-de-Grâce in Paris.

The identity of the celebrating priest “P. Adic, of the Diophantine Order” remained unclear. The most likely suspect was Helmut Hasse, but I couldn’t place him in Paris on June 3rd, 1939.

Hasse is the central figure in the picture above, taken in Oberwolfach in 1952, before one of his cars. Here’s another picture of car-freak Hasse (trains were to Andre Weil what cars were to Helmut Hasse). Both pictures are from the MFO photo collection.

Thanks to Peter Roquette’s publishing of Helmut Hasse’s letters we can now prove that Hasse was not in Paris on that particular day (however, he was there a couple of days earlier) but Weil had every reason to believe he might be there at the time he wrote the wedding invitation.

When was the wedding invitation written?

Frank Smithies recalls the spring 1939 period in Cambridge as follows :

“The climax of the academic year, as far as we were concerned, came in the Easter term. André Weil, Claude Chabauty, and Louis Bouckaert (from Louvain) were all in Cambridge, and the proposal was mooted that a marriage should be arranged between Bourbaki’s daughter Betti and Hector Pétard; the marriage announcement was duly printed in the canonical French style – on it Pétard was described as the ward of Ersatz Stanislas Pondiczery – and it was circulated to the friends of both parties. A couple of weeks later the Weils, Louis Bouckaert, Max Krook (a South African astrophysicist), Ralph and myself made a river excursion to Grantchester by punt and canoe to have tea at the Red Lion; there is a photograph of Ralph and myself, with our triumphantly captured lion between us and André Weil looking benevolently on.”

We know that this picture is taken on May 13th 1939 so the wedding-invitation was drawn up around mid april 1939.

“What did Weil know about Hasse’s visit to Paris?”

Hasse had been invited by Julia to give a series of lectures at the Institut Henri Poincare in 1938, but Hasse postponed his trip to Paris until May 1939.

In his letter to Hasse of January 20th 1939, Andre Weil writes:

“It is quite unfortunate that you couldn’t accept your invitation to Paris before this year, because last year all our number-theorists would have been present. By a sad coincidence all of us will be on travel this coming May (except for Chevalley perhaps who might have returned from the US by then). Pisot will be in Gottingen, Chabauty in Manchester visiting Mordell and I will be in Cambridge as I obtained a travel grant for England and Scandinavia.”

Clearly, Weil was aware of the upcoming visit of Hasse to Paris at the end of May, and there was no reason for him to assume that he wouldn’t be able to stay a weekend longer.

What do we know of Hasse’s visit to Paris?

Because Julia was exhausted and was on a three months sick leave, Elie Cartan took over the job of organising Hasse’s lecture series. In a letter of April 25th 1939 he proposes some possible dates, to which Hasse replies on April 30th 1939:

In it he fixes for the first time the dates of his talks which will be on “New results in the arithmetic of algebraic function fields” and consist of three lectures:

– On Friday 19th 1939: “Generalities: the group of divisor classes and the multiplier ring”

– On Saturday 20th 1939: “Rational and integral points on algebraic curves over the integers”

– On Tuesday 23rd 1939: “Rational points on algebraic curves with coefficient mod p”

He also mentions that he would stay for 15 days in Paris, arriving on May 17th, in time for the Jubilee Conference for Elie Cartan, scheduled on May 18th.

Weil must have known that Hasse would be present at the Cartan-fest and give a series of lectures in the following weeks. He had every reason to believe that Hasse would still be in Paris on Saturday June 3rd.

Where was Hasse on June 3rd 1939?

Back at home, as on that very day he wrote a letter to Henri Cartan, thanking him for an enjoyable day’s stay in Strasbourg, on the way back from Paris, on June 1st 1939:

If you want to catch up with previous posts on the Bourbaki wedding, you might want to download the booklet The Bourbaki Code.

16 ways to capture a lion (in 1938)

Published February 13, 2013 by lievenlb

A classic among mathematical jokes is the paper in the August/September 1938 issue of the American Mathematical Monthly “A contribution to the mathematical theory of big game hunting” by one Hector Petard of Princeton who would marry, one year later, Nicolas Bourbaki’s daughter Betti.

claimtoken-511b561b7a5a2

There are two main sources of information on the story behind this paper. There are Frank Smithies’ “Reminiscences of Ralph Boas” in the book Lion Hunting & Other Mathematical Pursuits and the transcript of an interview with John Tukey and Albert Tucker at Princeton University on 11 April 1984, part of the oral-history project on the Princeton mathematics community in the 1930s.

Smithies recalls being part of a lively group of people in Princeton during the academic year 1937/38 including Arthur Brown, Ralph Traber, Lyman Spitzer, Hugh Dowker, John Olmsted, Henry Walman, George Barnard, John Tukey, Mort Kanner (a physicist), Dick Jameson (a linguist) and Ralph Boas. Smithies writes:

“At some time that winter we were told about the mathematical methods for lion-hunting that have been devised in Gottingen, and several of us came up with new ones; who invented which method is now lost to memory. Ralph (Boas) and I decided to write up all the methods known to us, with a view to publication, conforming as closely as we could to the usual style of a mathematical paper. We choose H. Petard as a pseudonym (“the engineer, hoist with his own petard”; Hamlet, Act III, Scene IV), and sent the paper to the Americal Mathematical Monthly, over the signature of E. S. Pondiczery.”

Pondiczery was Princeton’s answer to Nicolas Bourbaki, and in the interview John Tukey recalls from (sometimes failing) memory:

“Well, the hope was that at some point Ersatz Stanislaus Pondiczery at the Royal Institute of Poldavia was going to be able to sign something ESP RIP. Then there’s the wedding invitation done by the Bourbakis. It was for the marriage of Betti Bourbaki and Pondiczery. It was a formal wedding invitation with a long Latin sentence, most of which was mathematical jokes, three quarters of which you could probably decipher. Pondiczery even wrote a paper under a pseudonym, namely “The Mathematical Theory of Big Game Hunting” by H. Petard, which appeared in the Monthly. There were also a few other papers by Pondiczery.”

Andrew Tucker then tells the story of the paper’s acceptance:

“Moulton, the editor of the Monthly at that time, wrote to me saying that he had this paper and the envelope was postmarked Princeton and he assumed that it was done by some people in math at Princeton. He said he would very much like to publish the paper, but there was a firm policy against publishing anything anonymous. He asked if I, or somebody else that he knew and could depend on, would tell him that the authorship would be revealed if for any reason it became legally necessary. I did not know precisely who they were, but I knew that John [Tukey] was one of them. He seemed to be in the thick of such things. John agreed that I could accept Moulton’s terms. I sent a letter with this assurance to Moulton and he went ahead and published it.”