Sociologists are a constant source of enlightenment as CNN keeps reminding
Kids who are turned
off by math often say they don’t enjoy it, they aren’t good
at it and they see little point in it. Who knew that could be a formula
for success?
The nations with the best scores have the
least happy, least confident math students, says a study by the
Brookings Institution’s Brown Center on Education Policy.
Countries reporting higher levels of enjoyment and confidence
among math students don’t do as well in the subject, the study
suggests.
The eighth-grade results reflected a common
pattern: The 10 nations whose students enjoyed math the most all scored
below average. The bottom 10 nations on the enjoyment scale all
excelled.
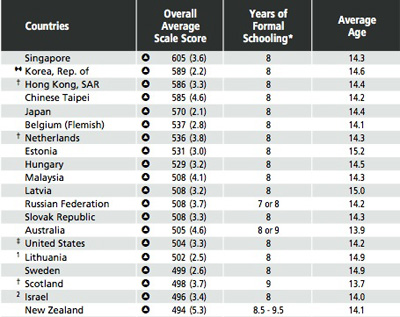
As this study is based on the 2003 Trends in International
Mathematics and Science Studies and as “we” scored best
of all western countries
this
probably explains all the unhappy faces in my first-year class on group
theory. However, they seemed quite happy the first few weeks.
Fortunately, this is proof, at least according to the mountain of wisdom, that I’m on the right track
If too many students are too happy in the math
classes, be sure that it is simply because not much is expected from
them. It can’t be otherwise. If teaching of mathematics is
efficient, it is almost guaranteed that a large group or a majority must
dislike the math classes. Mathematics is hard and if it is not hard, it
is not mathematics.
Right on! But then, why is
it that people willing to study maths enter university in a happy mood?
Oh, I get it, yes, it must be because in secondary school not much was
expected of them! Ouf! my entire world is consistent once again.
But then, hey wait, the next big thing that’s inevitably going to
happen is that in 2007 “we” will be tumbling down this world
ranking! And, believe it or not, that is precisely what
all my colleagues are eagerly awaiting to happen. Most of us are willing
to bet our annual income on it. Belgium was among the first countries to
embrace in the sixties-early seventies what was then called
“modern mathematics’ (you know: Venn-diagrams, sets,
topology, categories (mind you, just categories not the n-stuff ) etc.) Whole
generations of promising Belgian math students were able in the late
70ties, 80ties and early 90ties to do what they did mainly because of
this (in spite of graduating from ‘just’ a Belgian
university, only some of which make it barely in the times top 100 ). But
then, in the ’90ties politicians decided that mathematics had to
be sexed-up, only the kind of mathematics that one might recognize in
everyday life was allowed to be taught. For once, I have to
agree with motl.
Also, the attempts to connect mathematics with
the daily life are nothing else than a form of lowering of the
standards. They are a method to make mathematics more attractive for
those who like to talk even if they don’t know what they’re
talking about. They are a method to include mathematics between the
social and subjective sciences. They give a wiggle room to transform
happiness, confidence, common sense, and a charming personality into
good grades.
Indeed, the major problem we are
facing today in first year classes is that most students have no formal
training at all! An example : last week I did a test after three weeks
of working with groups. One of the more silly questions was to ask them
for precise definitions of very basic concepts (groups, subgroups,
cyclic groups, cosets, order of an element) : just 5 out of 44 were able
to do this! Most of them haven’t heard of sets at all. It seems
that some time ago it was decided that sets no longer had a place in
secondary school, so just some of them had at least a few lessons on
sets in primary school (you know the kind (probably you won’t but
anyway) : put all the green large triangles in the correct place in the
Venn diagram and that sort of things). Now, it seems that politicians
have decided that there is no longer a place for sets in primary schools
either! (And if we complain about this drastic lowering of
math-standards in schools, we are thrown back at us this excellent 2003
international result, so the only hope left for us is that we will fall
down dramatically in the 2007 test.) Mind you, they still give
you an excellent math-education in Belgian primary and secondary schools
provided you want to end up as an applied mathematician or (even worse)
a statistician. But I think that we, pure mathematicians, should
seriously consider recruiting students straight from Kindergarten!


