Skip to content →

Category: noncommutative

Manin’s three-space-2000

Published January 30, 2012 by lievenlb

Almost three decades ago, Yuri Manin submitted the paper “New dimensions in geometry” to the 25th Arbeitstagung, Bonn 1984. It is published in its proceedings, Springer Lecture Notes in Mathematics 1111, 59-101 and there’s a review of the paper available online in the Bulletin of the AMS written by Daniel Burns.

In the introduction Manin makes some highly speculative but inspiring conjectures. He considers the ring

$$\mathbb{Z}[x_1,\ldots,x_m;\xi_1,\ldots,\xi_n]$$

where $\mathbb{Z}$ are the integers, the $\xi_i$ are the “odd” variables anti-commuting among themselves and commuting with the “even” variables $x_j$. To this ring, Manin wants to associate a geometric object of dimension $1+m+n$ where $1$ refers to the “arithmetic dimension”, $m$ to the ordinary geometric dimensions $(x_1,\ldots,x_m)$ and $n$ to the new “odd dimensions” represented by the coordinates $(\xi_1,\ldots,\xi_n)$. Manin writes :

“Before the advent of ringed spaces in the fifties it would have been difficult to say precisely what me mean when we speak about this geometric object. Nowadays we simply define it as an “affine superscheme”, an object of the category of topological spaces locally ringed by a sheaf of $\mathbb{Z}_2$-graded supercommutative rings.”

Here’s my own image (based on Mumford’s depiction of $\mathsf{Spec}(\mathbb{Z}[x])$) of what Manin calls the three-space-2000, whose plain $x$-axis is supplemented by the set of primes and by the “black arrow”, corresponding to the odd dimension.

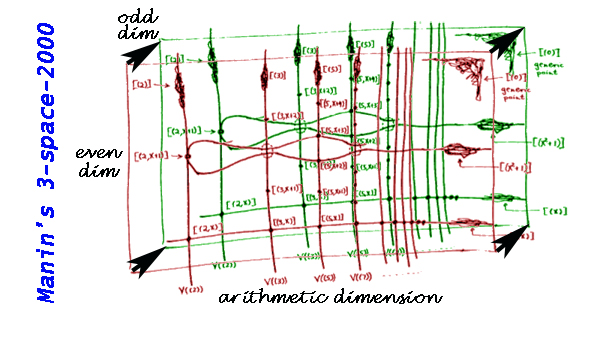
Manin speculates : “The message of the picture is intended to be the following metaphysics underlying certain recent developments in geometry: all three types of geometric dimensions are on an equal footing”.

Probably, by the addition “2000” Manin meant that by the year 2000 we would as easily switch between these three types of dimensions as we were able to draw arithmetic schemes in the mid-80ties. Quod non.

Twelve years into the new millenium we are only able to decode fragments of this. We know that symmetric algebras and exterior algebras (that is the “even” versus the “odd” dimensions) are related by Koszul duality, and that the precise relationship between the arithmetic axis and the geometric axis is the holy grail of geometry over the field with one element.

For aficionados of $\mathbb{F}_1$ there’s this gem by Manin to contemplate :

“Does there exist a group, mixing the arithmetic dimension with the (even) geometric ones?”

Way back in 1984 Manin conjectured : “There is no such group naively, but a ‘category of representations of this group’ may well exist. There may exist also certain correspondence rings (or their representations) between $\mathsf{Spec}(\mathbb{Z})$ and $x$.”

Leave a Comment

how noncommutative geometry shot itself

Published December 31, 2011 by lievenlb

I’ve never apologized for prolonged periods of blogsilence and have no intention to start now.

But, sometimes you need to expose the things holding you back before you can turn the page and (hopefully) start afresh.

Long time readers of this blog know I’ve often warned against group-think, personality cults and the making of exaggerate claims as possible threats to the survival of noncommutative geometry (for example in the group think post).

However, I was totally unprepared for this comment left on the noncommutative geometry blog, begin October:

Noncommutative Geometry is a field whose history is unpredictable.
When should I expect the pickaxe? Yours, Leon Trotsky

After sharing this on Google+ someone emailed suggesting I’d better have a look at some ‘semi-secret’ blogs. I did spend the better part of that friday going through more than 3 years worth of blogposts and cried my eyes out.

It is sad to read a message in a bottle and notice that after more than two years the matter is still far from resolved.

I wish you all a healing and liberating 2012!

Leave a Comment

Prep-notes dump

Published December 21, 2011 by lievenlb

Here are the scans of my crude prep-notes for some of the later seminar-talks. These notes still contain mistakes, most of them were corrected during the talks. So, please, read these notes with both mercy are caution!

Hurwitz formula imples ABC : The proof of Smirnov’s argument, but modified so that one doesn’t require an $\epsilon$-term. This is known to be impossible in the number-theory case, but a possible explanation might be that not all of the Smirnov-maps $q~:~\mathsf{Spec}(\mathbb{Z}) \rightarrow \mathbb{P}^1_{\mathbb{F}_1}$ are actually covers.

Frobenius lifts and representation rings : Faithfully flat descent allows us to view torsion-free $\mathbb{Z}$-rings with a family of commuting Frobenius lifts (aka $\lambda$-rings) as algebras over the field with one element $\mathbb{F}_1$. We give several examples including the two structures on $\mathbb{Z}[x]$ and Adams operations as Frobenius lifts on representation rings $R(G)$ of finite groups. We give an example that this extra structure may separate groups having the same character table. In general this is not the case, the magic Google search term is ‘Brauer pairs’.

Big Witt vectors and Burnside rings : Because the big Witt vectors functor $W(-)$ is adjoint to the tensor-functor $- \otimes_{\mathbb{F}_1} \mathbb{Z}$ we can view the geometrical object associated to $W(A)$ as the $\mathbb{F}_1$-scheme determined by the arithmetical scheme with coordinate ring $A$. We describe the construction of $\Lambda(A)$ and describe the relation between $W(\mathbb{Z})$ and the (completion of the) Burnside ring of the infinite cyclic group.

Density theorems and the Galois-site of $\mathbb{F}_1$ : We recall standard density theorems (Frobenius, Chebotarev) in number theory and use them in combination with the Kronecker-Weber theorem to prove the result due to James Borger and Bart de Smit on the etale site of $\mathsf{Spec}(\mathbb{F}_1)$.

New geometry coming from $\mathbb{F}_1$ : This is a more speculative talk trying to determine what new features come up when we view an arithmetic scheme over $\mathbb{F}_1$. It touches on the geometric meaning of dual-coalgebras, the Habiro-structure sheaf and Habiro-topology associated to $\mathbb{P}^1_{\mathbb{Z}}$ and tries to extend these notions to more general settings. These scans are unintentionally made mysterious by the fact that the bottom part is blacked out (due to the fact they got really wet and dried horribly). In case you want more info, contact me.

Leave a Comment