Skip to content →

Category: math

the moonshine picture – at last

Published January 23, 2018 by lievenlb

The monstrous moonshine picture is the subgraph of Conway’s big picture consisting of all lattices needed to describe the 171 moonshine groups.

It consists of:

– exactly 218 vertices (that is, lattices), out of which

– 97 are number-lattices (that is of the form $M$ with $M$ a positive integer), and

– 121 are proper number-like lattices (that is of the form $M \frac{g}{h}$ with $M$ a positive integer, $h$ a divisor of $24$ and $1 \leq g \leq h$ with $(g,h)=1$).

The $97$ number lattices are closed under taking divisors, and the corresponding Hasse diagram has the following shape

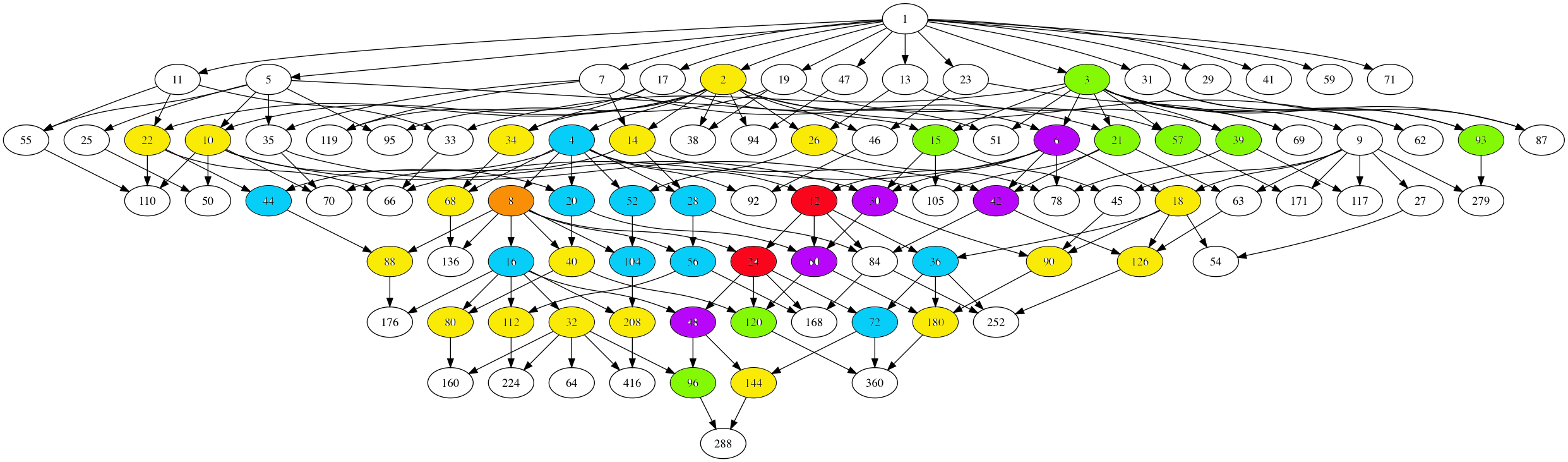
Here, number-lattices have the same colour if they have the same local structure in the moonshine picture (that is, have a similar neighbourhood of proper number-like lattices).

There are 7 different types of local behaviour:

The white numbered lattices have no proper number-like neighbours in the picture.

The yellow number lattices (2,10,14,18,22,26,32,34,40,68,80,88,90,112,126,144,180,208 = 2M) have local structure

\[
\xymatrix{M \ar@{-}[r] & \color{yellow}{2M} \ar@{-}[r] & M \frac{1}{2}} \]

which involves all $2$-nd (square) roots of unity centered at the lattice.

The green number lattices (3,15,21,39,57,93,96,120 = 3M) have local structure

\[
\xymatrix{& M \ar@[red]@{-}[d] & \\ M \frac{1}{3} \ar@[red]@{-}[r] & \color{green}{3M} \ar@[red]@{-}[r] & M \frac{2}{3}} \]

which involve all $3$-rd roots of unity centered at the lattice.

The blue number lattices (4,16,20,28,36,44,52,56,72,104 = 4M) have as local structure

\[
\xymatrix{M \frac{1}{2} \ar@{-}[d] & & M \frac{1}{4} \ar@{-}[d] \\
2M \ar@{-}[r] & \color{blue}{4M} \ar@{-}[r] & 2M \frac{1}{2} \ar@{-}[d] \\
M \ar@{-}[u] & & M \frac{3}{4}} \]

and involve the $2$-nd and $4$-th root of unity centered at the lattice.

The purple number lattices (6,30,42,48,60 = 6M) have local structure

\[
\xymatrix{& M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} & M \frac{1}{6} \ar@[red]@{-}[d] & \\
M \ar@[red]@{-}[r] & 3M \ar@{-}[r] \ar@[red]@{-}[d] & \color{purple}{6M} \ar@{-}[r] \ar@[red]@{-}[u] \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@[red]@{-}[r] \ar@[red]@{-}[d] & M \frac{5}{6} \\
& M \frac{2}{3} & 2M \frac{2}{3} & M \frac{1}{2} & } \]

and involve all $2$-nd, $3$-rd and $6$-th roots of unity centered at the lattice.

The unique brown number lattice 8 has local structure

\[
\xymatrix{& & 1 \frac{1}{4} \ar@{-}[d] & & 1 \frac{1}{8} \ar@{-}[d] & \\
& 1 \frac{1}{2} \ar@{-}[d] & 2 \frac{1}{2} \ar@{-}[r] \ar@{-}[d] & 1 \frac{3}{4} & 2 \frac{1}{4} \ar@{-}[r] & 1 \frac{5}{8} \\
1 \ar@{-}[r] & 2 \ar@{-}[r] & 4 \ar@{-}[r] & \color{brown}{8} \ar@{-}[r] & 4 \frac{1}{2} \ar@{-}[d] \ar@{-}[u] & \\
& & & 1 \frac{7}{8} \ar@{-}[r] & 2 \frac{3}{4} \ar@{-}[r] & 1 \frac{3}{8}} \]

which involves all $2$-nd, $4$-th and $8$-th roots of unity centered at $8$.

Finally, the local structure for the central red lattices $12,24 = 12M$ is

\[
\xymatrix{
M \frac{1}{12} \ar@[red]@{-}[dr] & M \frac{5}{12} \ar@[red]@{-}[d] & M \frac{3}{4} \ar@[red]@{-}[dl] & & M \frac{1}{6} \ar@[red]@{-}[dr] & M \frac{1}{2} \ar@[red]@{-}[d] & M \frac{5}{6} \ar@[red]@{-}[dl] \\
& 3M \frac{1}{4} \ar@{-}[dr] & 2M \frac{1}{6} \ar@[red]@{-}[d] & 4M \frac{1}{3} \ar@[red]@{-}[d] & 2M \frac{1}{3} \ar@[red]@{-}[d] & 3M \frac{1}{2} \ar@{-}[dl] & \\
& 2M \frac{1}{2} \ar@[red]@{-}[r] & 6M \frac{1}{2} \ar@{-}[dl] \ar@[red]@{-}[d] \ar@{-}[r] & \color{red}{12M} \ar@[red]@{-}[d] \ar@{-}[r] & 6M \ar@[red]@{-}[d] \ar@{-}[dr] \ar@[red]@{-}[r] & 2M & \\
& 3M \frac{3}{4} \ar@[red]@{-}[dl] \ar@[red]@{-}[d] \ar@[red]@{-}[dr] & 2M \frac{5}{6} & 4M \frac{2}{3} & 2M \frac{2}{3} & 3M \ar@[red]@{-}[dl] \ar@[red]@{-}[d] \ar@[red]@{-}[dr] & \\
M \frac{1}{4} & M \frac{7}{12} & M \frac{11}{12} & & M \frac{1}{3} & M \frac{2}{3} & M}
\]

It involves all $2$-nd, $3$-rd, $4$-th, $6$-th and $12$-th roots of unity with center $12M$.

No doubt this will be relevant in connecting moonshine with non-commutative geometry and issues of replicability as in Plazas’ paper Noncommutative Geometry of Groups like $\Gamma_0(N)$.

Another of my pet follow-up projects is to determine whether or not the monster group $\mathbb{M}$ dictates the shape of the moonshine picture.

That is, can one recover the 97 number lattices and their partition in 7 families starting from the set of element orders of $\mathbb{M}$, applying some set of simple rules?

One of these rules will follow from the two equivalent notations for lattices, and the two different sets of roots of unities centered at a given lattice. This will imply that if a number lattice belongs to a given family, certain divisors and multiples of it must belong to related families.

If this works out, it may be a first step towards a possibly new understanding of moonshine.

Leave a Comment

Knights and Knaves, the Heyting way

Published January 22, 2018 by lievenlb

(image credit: Joe Blitzstein via Twitter)

Smullyan’s Knights and Knaves problems are classics. On an island all inhabitants are either Knights (who only tell true things) and Knaves (who always lie). You have to determine their nature from a few statements. Here’s a very simple problem:

“Abercrombie met just two inhabitants, A and B. A made the following statement: “Both of us are Knaves.” What is A and what is B?”

Now, this one is simple enough to solve, but for more complicated problems a generic way to solve the puzzles is to use propositional calculas, as explained in Smullyan’s Logical Labyrinths”, chapter 8 “Liars, truth-tellers and propositional logic’.

If an inhabitants $A$ asserts a proposition $P$, and if $k_A$ is the assertion ‘$A$ is a Knight’, then the statement can be rephrased as

\[
k_A \Leftrightarrow P \]

for if $A$ is a Knight, $P$ must be true and if $A$ is a Knave $P$ must be false.

Usually, one can express $P$ as a propositional statement involving $k_A,k_B,k_C,\dots$.
The example above can be rephrased as

\[
k_A \Leftrightarrow (\neg k_A \wedge \neg k_B) \]

Assigning truth values to $k_A$ and $k_B$ and setting up the truth-table for this sentence, one sees that the only possibility for this to be true is that $k_A$ equals $0$ and $k_B$ equals $1$. So, $A$ is a Knave and $B$ is a Knight.

Clearly, one only requires this approach for far more difficult problems.

In almost all Smullyan puzzles, the only truth values are $0$ and $1$. There’s a short excursion to Boolean algebras (sorry, Boolean islands) in chapter 9 ‘Variable Liars’ in Logical Labyrinths. But then, the type of problems are about finding equivalent notions of Boolean algebras, rather that generalised Knights&Knaves puzzles.

Did anyone pursue the idea of Smullyanesque puzzles with truth values in a proper Heyting algebra?

I only found one blog-post on this: Non-Classical Knights and Knaves by Jason Rosenhouse.

He considers three valued logic (the Heyting algebra corresponding to the poset 0-N-1, and logical connectives as in the example on the Wiki-page on Heyting algebras.

On his island the natives cycle, repeatedly and unpredictably, between the two states. They are knights for a while, then they enter a transitional phase during which they are partly knight and partly knave, and then they emerge on the other side as knaves.

“If Joe is in the transitional phase, and you say, “Joe is a knight,” or “Joe is a knave,” what truth value should we assign to your statement? Since Joe is partly knight and partly knave, neither of the classical truth values seems appropriate. So we shall assign a third truth value, “N” to such statements. Think of N as standing for “neutral” or “neither true nor false.” On the island, vague statements are assigned the truth value N.

Just to be clear, it’s not just any statement that can be assigned the truth value N. It is only vague statements that receive that truth value, and for now our only examples of such statements are attributions of knight-hood and knave-hood to people in the transitional phase.

For the natives, entering the transitional phase implied a disconcerting loss of identity. Uncertain of how to behave, they hedged their bets by only making statements with truth value N. People in the transitional phase were referred to as neutrals. So there are now three kinds of people: Knights, who only make true statements; Knaves, who only make false statements; and Neutrals, who only make statements with the truth value N.”

He gives one example of a possible problem:

“Suppose you meet three people, named Dave, Evan and Ford. They make the following statements:

Dave: Evan is a knight.
Evan: Ford is a knave.
Ford: Dave is a neutral.

Can you determine the types of all three people?”

If you know of more of these Smullanesque problems using Heyting algebras, please leave a comment.

Leave a Comment

a non-commutative Jack Daniels problem

Published January 20, 2018 by lievenlb

At a seminar at the College de France in 1975, Tits wrote down the order of the monster group

\[
\# \mathbb{M} = 2^{46}.3^{20}.5^9.7^6.11^2.13^3.17·19·23·29·31·41·47·59·71 \]

Andrew Ogg, who attended the talk, noticed that the prime divisors are precisely the primes $p$ for which the characteristic $p$ super-singular $j$-invariants are all defined over $\mathbb{F}_p$.

Here’s Ogg’s paper on this: Automorphismes de courbes modulaires, Séminaire Delange-Pisot-Poitou. Théorie des nombres, tome 16, no 1 (1974-1975).

Ogg offered a bottle of Jack Daniels for an explanation of this coincidence.

Even Richard Borcherds didn’t claim the bottle of Jack Daniels, though his proof of the monstrous moonshine conjecture is believed to be the best explanation, at present.

A few years ago, John Duncan and Ken Ono posted a paper “The Jack Daniels Problem”, in which they prove that monstrous moonshine implies that if $p$ is not one of Ogg’s primes it cannot be a divisor of $\# \mathbb{M}$. However, the other implication remains mysterious.

Duncan and Ono say:

“This discussion does not prove that every $p ∈ \text{Ogg}$ divides $\# \mathbb{M}$. It merely explains how the first principles of moonshine suggest this implication. Monstrous moonshine is the proof. Does this then provide a completely satisfactory solution to Ogg’s problem? Maybe or maybe not. Perhaps someone will one day furnish a map from the characteristic $p$ supersingular $j$-invariants to elements of order $p$ where the group structure of $\mathbb{M}$ is apparent.”

I don’t know whether they claimed the bottle, anyway.

But then, what is the non-commutative Jack Daniels Problem?

A footnote on the first page of Conway and Norton’s ‘Monstrous Moonshine’ paper says:

“Very recently, A. Pizer has shown these primes are the only ones that satisfy a certain conjecture of Hecke from 1936 relating modular forms of weight $2$ to quaternion algebra theta-series.”

Pizer’s paper is “A note on a conjecture of Hecke”.

Maybe there’s a connection between monstrous moonshine and the arithmetic of integral quaternion algebras. Some hints:

The commutation relations in the Big Picture are reminiscent of the meta-commutation relations for Hurwitz quaternions, originally due to Conway in his booklet on Quaternions and Octonions.

The fact that the $p$-tree in the Big Picture has valency $p+1$ comes from the fact that the Brauer-Severi of $M_2(\mathbb{F}_p)$ is $\mathbb{P}^1_{\mathbb{F}_p}$. In fact, the Big Picture should be related to the Brauer-Severi scheme of $M_2(\mathbb{Z})$.

Then, there’s Jorge Plazas claiming that Connes-Marcolli’s $GL_2$-system might be related to moonshine.

One of the first things I’ll do when I return is to run to the library and get our copy of Shimura’s ‘Introduction to the arithmetic theory of automorphic functions’.

Btw. the bottle in the title image is not a Jack Daniels but the remains of a bottle of Ricard, because I’m still in the French mountains.

Leave a Comment