As you may have guessed from the symmetries of Covid-19 post, I did spend some time lately catching up with the literature on the geometric structure and symmetries of viruses. It may be fun to run a little series on this.
A virus is a parasite, so it cannot reproduce on its own and needs to invade a host cell to replicate. All information needed for this replication process is stored in a fragile DNA or RNA string, the viral genome.
This genome needs to be protected by a coating made of proteins, the viral capsid. Most viruses have an additional fatty protection layer, the envelope, decorated by virus (glyco)proteins (such as the ‘spikes’ needed to infiltrate the host cell).
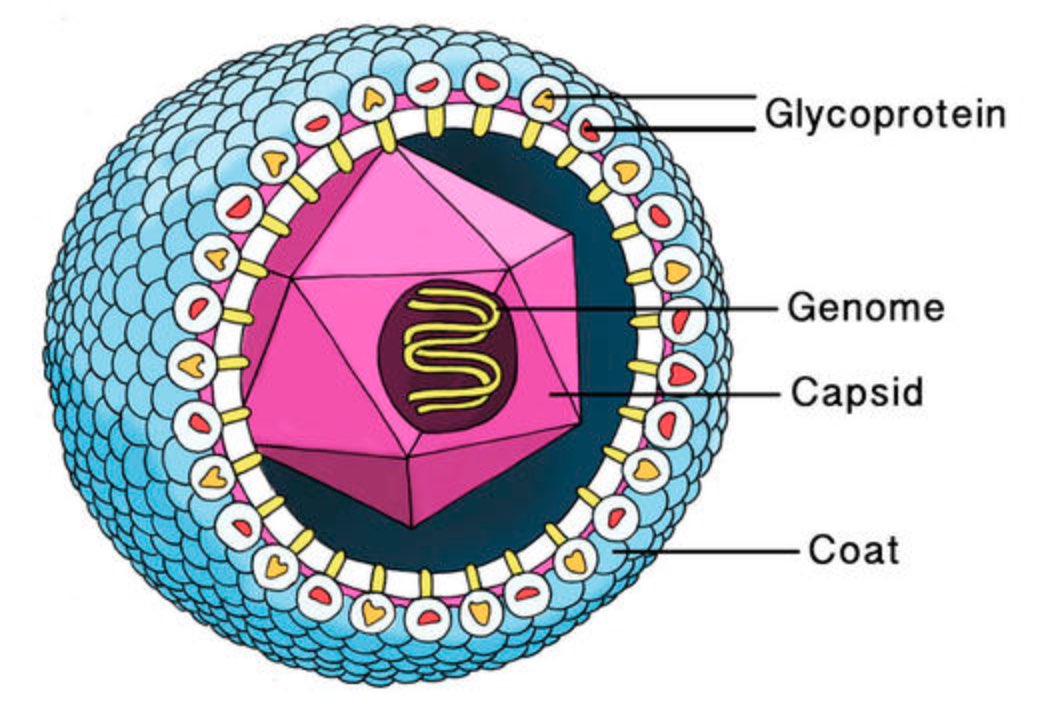
Most viruses are extremely small (between 20 and 200nm), our friend the corona-virus measures between 80 and 120nm. So, its genome is also pretty small (the corona genome has around 30.000 base pairs). To maximise its information, the volume of the protective capsid must be as large as possible, and must be formed by just a few different proteins (to free as much space in the code of the genome for other operations) and clusters of them are distributed over the polyhedral capsid, as symmetric as possible.
This insight led Watson and Crick, the discoverers of the structure of DNA, to the ‘genetic economy’-proposal that most sphere-like viruses will have an icosahedral capsid because the icosahedron is the Platonic solid with the largest volume and rotational symmetry group. They argued that the capsid is most likely constructed from a single subunit (capsomere), which is repeated many times to form the protein shell.
Little is known about capsid formation, that is the process in which the capsid proteins self-assemble into an icosahedral shape, nor about the precise interplay between the genome and the capsid proteins. If we would understand these two things better it might open new possibilities for anti-viral drugs, by either blocking the self-assembly process or by breaking the genome-capsid interaction.
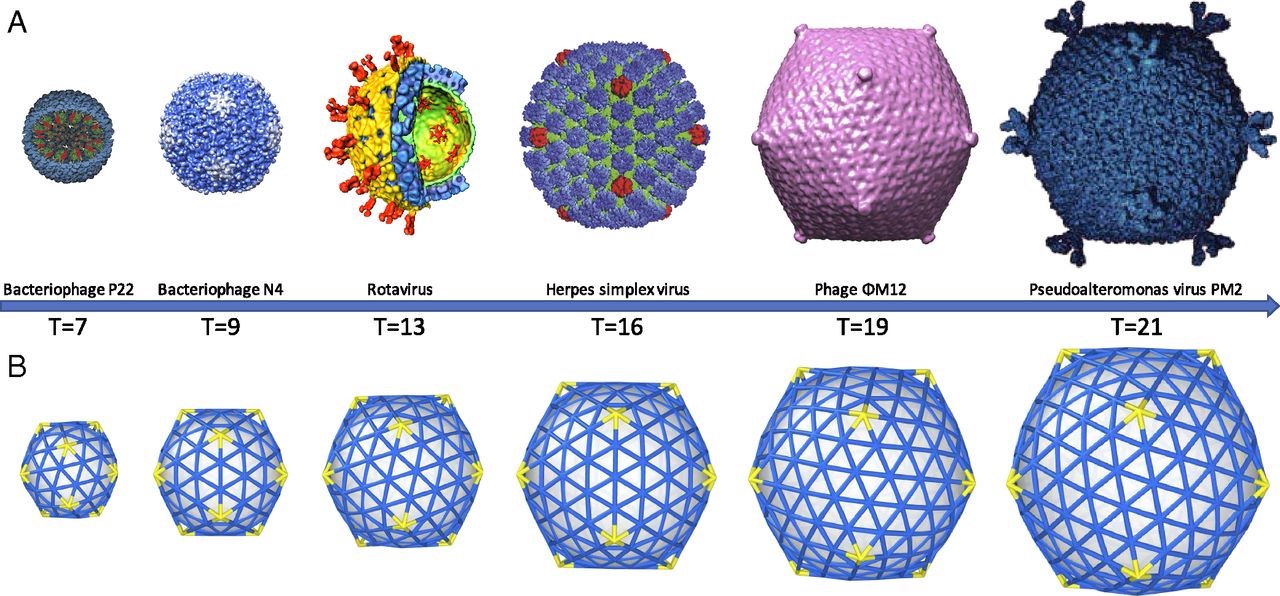
A first proposal for the capsid structure was put forward by Caspar and Klug. Their quasi-equivalence principle asserts that each of the 20 triangular faces of the icosahedron is subdivided in 3 subunits, each consisting of at least one protein.
Most viruses have much more than 60 proteins in their capsid, so Caspar and Klug introduced their $T$-number giving the number of proteins per subunit. One superimposes the triangulation of the icosahedron with the hexagonal plane lattice, then $T$ is the number of sub-triangles of these hexagons contained in each subunit. For $T = 7$ we have the following situation
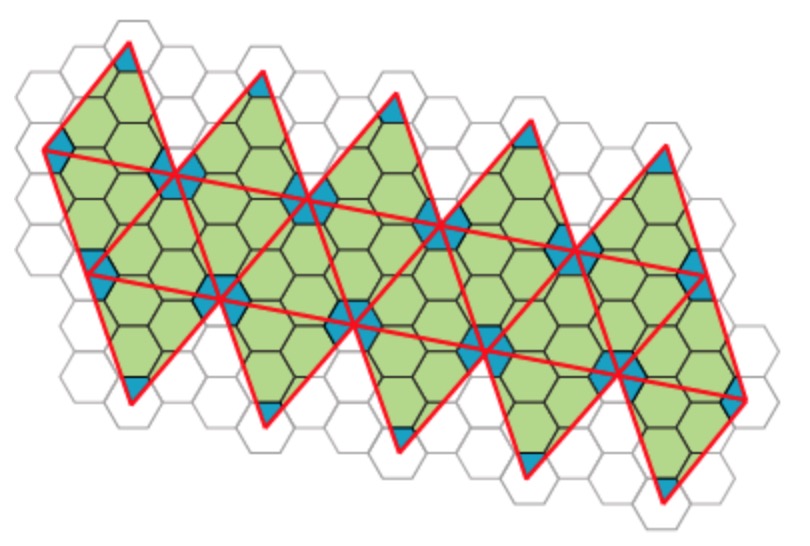
Folding back the triangulation to form the icosahedron one then obtains a tiling consisting of hexagons (the green regions) and pentagons (the blue regions)

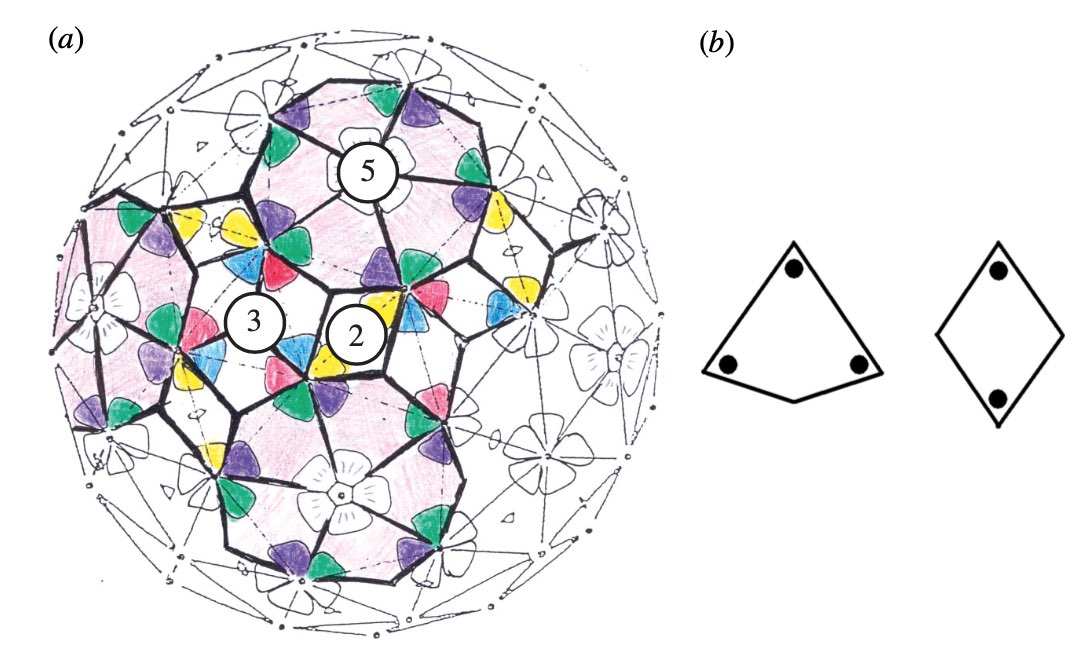
It turned out that many viruses with icosahedral symmetry consist of subunits having a different number of proteins, such as dimers (2 proteins), trimers (3 proteins), or pentamers (5 proteins) and these self-organise around a 2, 3, or 5-fold rotational axis of the icosahedron.
This led Reidun Twarock around 2000 to propose her virus tiling theory. This is a generalisation of the Caspar-Klug theory in which one superimposese the triangulation of the icosahedron with other tilings of the plane, consisting of two or more non-congruent tiles. Here an example which looks a bit like the aperiodic Penrose tilings of the plane.
Here’s a recent Quanta-Magazine article on Twarock’s work and potential consequences: The illuminating geometry of viruses.
And here’s an LMS Popular Lecture, from 2008, by Raidun Twarock herself: “Know your enemy – viruses under the mathematical microscope”.
Leave a Comment
