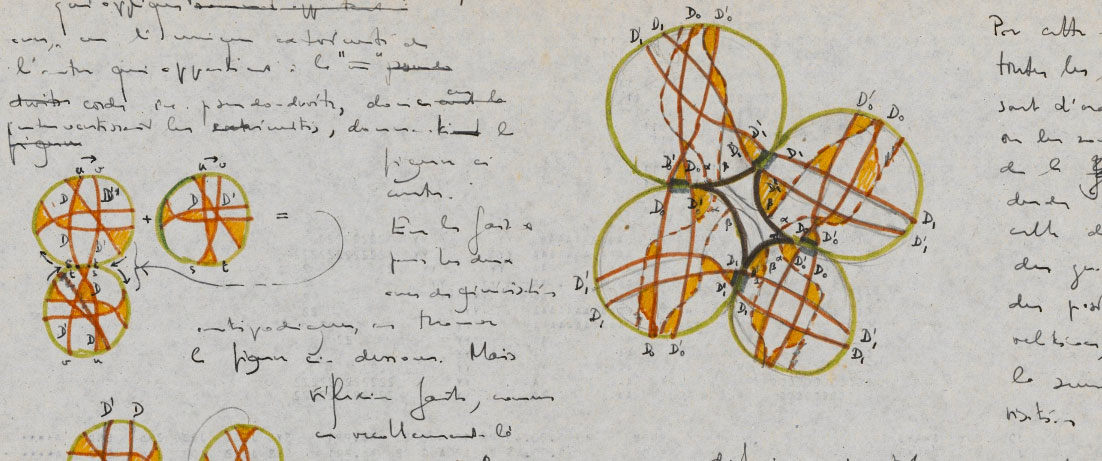Category: web

Lockdown reading : the Carls

Published February 28, 2021 by lievenlb

In this series I’ll mention some books I found entertaining, stimulating or comforting during these Corona times. Read them at your own risk.

An Absolutely Remarkable Thing (AART for the fans) by Hank Green came out in 2018, and recently I reread it when its sequel A Beautifully Foolish Endeavor appeared last summer.

“Protagonist April May discovers a large robot sculpture in Midtown Manhattan. She and her friend Andy Skampt decide to film it and post the video online, which goes viral and makes April an overnight celebrity. All over the world identical structures—known as “Carls”—have appeared in major cities at exactly the same time.” (Wikipedia)

Here’s an artist’s impression of said video, followed by the ‘Queen sequence’ (one of many puzzles in the book). On an audio fragment a faint trace of Queen’s “Don’t Stop Me Now” is heard, and April discovers the code “IAMU” after fixing a series of typos in the Wikipedia article about that song.

Three reasons why you might want to read this book now:

It’s about the dangers and pitfalls of social media and online fame. (Something Hank Green is familiar with as he runs with his brother the YouTube channel Vlogbrothers.)
It’s about a global pandemic. (Not caused by a virus, but by a contagious dream, containing 4096 ‘sequences’=puzzles, each resulting in an HEX-sequence to be combined into a vector-image.)
It’s about the consequences of hate speech. (It’s hard not to draw parallels between ‘Peter Petrawicki’ and a former president, and between the actions of the ‘Defenders’ and the events of January 6th.)

AART doesn’t end well for April May, and it was hard to image Hank Green ever writing a sequel without doing a Bobby Ewing shower scene (showing my age here). And yes, the book ends with a two word text message from April: “Knock Knock”.

The sequel ‘A Beautifully Foolish Endeavour’ is perhaps even more enjoyable than AART. The Dream is now replaced by a Magic Book, and the storytelling (at first) no longer done by April herself but by her four evangelists (Maya, Andy, Miranda and Robin), Green’s very own Mamalujo so to speak.

G+ recovery 6 : math-history

Published February 6, 2019 by lievenlb

In April my Google+ account will disappear. Here I collect some G+ posts, in chronological order, having a common theme. Today, math-history (jokes and puns included).

September 20th, 2011

Was looking up pictures of mathematicians from the past and couldn’t help thinking ‘Hey, I’ve seen this face before…’

Leopold Kronecker = DSK (2/7/2019 : DSK = Dominique Strauss-Kahn)

Adolf Hurwitz = Groucho Marx

June 2nd, 2012

The ‘Noether boys’

(Noether-Knaben in German) were the group of (then) young algebra students around Emmy Noether in the early 1930’s. Actually two of them were girls (Grete Hermann and Olga Taussky).

The picture is taken from a talk Peter Roquette gave in Heidelberg. Slides of this talk are now available from his website.

In 1931 Jacques Herbrand (one of the ‘Noether boys’) fell to his death while mountain-climbing in the Massif des Écrins (France). He was just 23, but already considered one of the greatest minds of his generation.

He introduced the notion of recursive functions while proving “On the consistency of arithmetic”. In several texts on Herbrand one finds this intriguing quote by Chevalley (one of the first generation Bourbakis):

“Jacques Herbrand would have hated Bourbaki” said French mathematician Claude Chevalley quoted in Michèle Chouchan “Nicolas Bourbaki Faits et légendes” Edition du choix, 1995. («Jacques Herbrand aurait détesté Bourbaki» in the original French version).

Can anyone tell me the underlying story?

June 26th, 2012

a 3yr old post on Scottish vs. Platonic Solids did hit Reddit/pics

1.4k upvotes. Surreal!

I’d better point them to the latest on this then.

Scottish solids, final(?) comments.

The return of the Scottish solids

December 19th, 2012

Mumford’s treasure map

+Pieter Belmans (re)discovered a proto-drawing of Mumford’s iconic map of Spec(Z[x]) in his ‘red book’.

The proto-pic is taken from Mumford’s ‘Lectures on curves on an algebraic surface’ p.28 and tries to depict the integral projective line. The set-up is rather classical (focussing on points of different codimension) whereas the red-book picture is more daring and has been an inspiration for generations of arithmetical geometers.

Still there’s the issue of dating these maps.

Mumford himself dates the P^1 drawing 1964 (although the publication date is 66) and the red-book as 1967.

Though I’d love to hear more precise dates, I’m convinced they are about right. In the ‘Curves’-book’s preface Mumford apologises to ‘any reader who, hoping that he would find here in these 60 odd pages an easy and concise introduction to schemes, instead becomes hopelessly lost in a maze of unproven assertions and undeveloped suggestions.’ and he stresses by underlining ‘From lecture 12 on, we have proven everything that we need’.

So, clearly the RedBook was written later, and as he has written in-between his master-piece GIT i’d say Mumford’s own dating is about right.

Still, it is not a completely vacuous dispute as the ‘Curves’ book (supposedly from 1964 or earlier) contains a marvelous appendix by George Bergman on the Witt ring which would predate Cartier’s account…

Thanks to +James Borger i know of George’s take on this

“I was a graduate student taking the course Mumford gave on curves and surfaces; but algebraic geometry was not my main field, and soon into the course I was completely lost. Then Mumford started a self-contained topic that he was going to weave in — ring schemes — and it made clear and beautiful sense to me; and when he constructed the Witt vector ring scheme, I thought about it, saw a nicer way to do it, talked with him about it and with his permission presented it to the class, and eventually wrote it up as a chapter in his course notes.
I think that my main substantive contribution was the tying together of the various prime-specific ring schemes into one big ring scheme that works for all primes. The development in terms of power series may or may not have originated with me; I just don’t remember.”

which sounds very Bergmannian to me.

Anyway I’d love to know more about the dating of the ‘Curves’ book and (even more) the first year Mumford delivered his Red-Book-Lectures (my guess 1965-66). Thanks.
Pieter maintains an “Atlas of this picture” here

June 17th, 2013

the birthday of schemes : november 5th 1956

The wikipedia-entry linking Andre Martineau to the origin of the scheme-concept appears to rely on footnote 29 of Cartier’s ‘A mad day’s work, from Grothendieck to Connes and Kontsevich’ which reads:

“Serre first considered the set of maximal ideals of a commutative ring A subject to certain restrictions. Martineau then remarked to him that his arguments remained valid for any commutative ring, provided one takes all prime ideals instead of only maximal ideals. I then proposed a definition of schemes equivalent to the definition of Grothendieck. In my dissertation I confined myself to a framework similar to that of Chevalley, so as to avoid an excessively long exposition of the preliminaries!”

In the 1956/57 Chevalley seminar Cartier gave the first two talks and in the first one, on november 5th 1956, one finds the first published use of the word ‘scheme’, which he refers to as ‘schemes in the sense of Chevalley-Nagata’. On page 9 of that talk he introduces the prime spectrum with its Zariski topology.

In the second talk a week later, on november 12th, he then gives the general definition of a scheme (as we know it, by gluing together affine schemes and including the stalks).

BUT, he did all of this ‘only’ for affine rings over a field, ‘to avoid an excessively long exposition of the preliminaries’…

Grothendieck then made the quantum-leap to general commutative rings.

June 18th, 2013

Correction : scheme-birthday = december 12th, 1955

Claude Chevalley gave already two talks on ‘Schemes’ in the Cartan-Chevalley seminar of 1955/56, the first one on december 12th 1955, the other a week later.

Chevalley only considers integral schemes, of finite type over a field (Cartier drops the integrality condition on november 5th 1956, a bit later Grothendieck will drop all restrictions).

Grothendieck’s quote “But then, what are schemes?” uttered in a Parisian Cafe must date from that period. Possibly Cartier explained the concept to him. In a letter to Serre, dated december 15th 1955, Grothendieck is quite impressed with Cartier:

“Cartier seems to be an amazing person, especially his speed of understanding, and the incredible amount of things he reads and grasps; I really have the impression that in a few years he will be where you are now. I am exploiting him most profitably.”

June 18th, 2013

David Mumford on the Italian school of Geometry

Short version:
Castelnuovo : the good
Severi : the bad
Enriques : the ugly

The longer version:

“The best known case is the Italian school of algebraic geometry, which produced extremely good and deep results for some 50 years, but then went to pieces.
There are 3 key names here — Castelnuovo, Enriques and Severi.

C was earliest and was totally rigorous, a splendid mathematician.

E came next and, as far as I know, never published anything that was false, though he openly acknowledged that some of his proofs didn’t cover every possible case (there were often special highly singular cases which later turned out to be central to understanding a situation). He used to talk about posing “critical doubts”. He had his own standards and was happy to reexamine a “proof” and make it more nearly complete.

Unfortunately Severi, the last in the line, a fascist with a dictatorial temperament, really killed the whole school because, although he started off with brilliant and correct discoveries, later published books full of garbage (this was in the 30’s and 40’s). The rest of the world was uncertain what had been proven and what not. He gave a keynote speech at the first Int Congress after the war in 1950, but his mistakes were becoming clearer and clearer.

It took the efforts of 2 great men, Zariski and Weil, to clean up the mess in the 40’s and 50’s although dredging this morass for its correct results continues occasionally to this day.” (David Mumford)

June 19th, 2014

Hirune Mendebaldeko – Bourbaki’s muse

After more than 70 years, credit is finally given to a fine, inspiring and courageous Basque algebraic geometer.

One of the better held secrets, known only to the first generation Bourbakistas, was released to the general public in april 2012 at the WAGS Spring 2012, the Western Algebraic Geometry Symposium, held at the University of Washington.

Hirune Mendebaldeko was a Basque pacifist, a contemporary of Nicholas Bourbaki, whom she met in Paris while there studying algebraic geometry. They were rumored to be carrying on a secret affair, with not infrequent trysts in the Pyrenees. Whenever they appeared together in public, however, there was no indication of any personal relationship.

From the comments, by +Sandor Kovacs:

+Chris Brav Chris, just between us: the whole thing is a joke. I just tried to put yet another twist on it. Also, until now we have never admitted that it is, so please don’t tell anyone. 😉

The explanation at the end of +lieven lebruyn’s blog post was indeed the original motivation for the name. We were starting a new “named” lecture series as part of WAGS and wanted to name it after someone not obvious. Basque is a language not related to any other. It seemed a good idea to use that, so very few people would know the meaning of any particular word.

Then we tried all the words in WAGS, but the other three were actually very similar to the English/etc versions. The first name was chosen by vibe. Then we decided that we needed a bio for our distinguished namesake and the connection to Bourbaki presented itself for various reasons that you can guess. But we wanted a pacifist and it seemed a nice contrast to Bourbaki. So Hirune was born and we were hoping that one day she would gain prominence in the world. Finally, it happened. 🙂

June 22nd, 2014

the state of European mathematics in 1927

This map, from the Rockefeller foundation, gives us the top 3 mathematical institutes in 1927 : Goettingen, Paris and … Rome.
The pie-charts per university show that algebra was a marginal topic then (wondering how a similar map might look today).

December 1st, 2015

Did Chevalley invent the Zariski topology?

In his inaugural lecture at #ToposIHES Pierre Cartier stated (around 44m11s):
“By the way, Zariski topology, as we know it today, was not what Zariski invented. He invented a variant of that, a topology on the set of all valuation rings of a given field, which is not exactly the same thing. As for the Zariski topology, the rumour is that it was invented by Chevalley in a seminar given by Zariski, but I have no real proof.”
Do you know more about this?

Btw. the full lecture of Cartier (mostly on sheaf theory) is not on the IHES YouTube channel, but on the channel of +Laurence Honnorat.

The IHES did begin to upload videos of the remaining plenary talks
here (so far, the wednesday talks are available).

G+ recovery 2 : Grothendieck

Published February 3, 2019 by lievenlb

My Google+ account is going away on April 2, 2019, so i’ll try to rescue here some posts, in chronological order and around one theme. Here’s Grothendieck-stuff, part two.

March 18th, 2014

crowd-funding Grothendiecks biography?

+John Baez has a post out at the n-cat-cafe on Leila Schneps’s quest to raise $6000 to translate Scharlau’s 3-volume biography of Grothendieck.

If you care to contribute : go here.

Lots of good stuff in volume 3 on Groths hippy/eco/weirdo years. I’ve plundered Scharlau’s text last year trying to pinpoint the location of Groths hideout in the French Pyrenees.

As far as i know, part 2 (the most interesting part on Groths mathematical years) is still under construction and will be compiled by the jolly group called the “Grothendieck circle”.

There’s a nice series of G-recollections out here (a.o. by Illusie, Karoubi, Cartier, Raynaud, Mumford, Hartshorne, Murre, Oort, Manin, Cartier).

I’m pretty sure Groth himself would prefer we’d try to get his Recoltes et Semailles translated into English, or La Clef des Songes.

November 18th, 2014

Grothendieck’s last hideout

The past ten days I’ve been up in the French mountains (without internet access), not that far from the Ariege, so I’m just now catching up with all (blog)posts related to Grothendieck’s death.

At our place, the morning of thursday november 13th was glorious!

Even though FranceInter kept telling horror stories about flooding in more southern departements, I can only hope that Grothendieck passed away in that morning sun.
About a year ago, on the occasion of Groth’s 85th birthday, I ran a series of posts on places where he used to live, ending with his last known hideout

At the time I didn’t include the precise location of his house, but now that pictures of it are in the French press I feel free to suggest (if you are interested to know where Grothendieck spend his later years) to point your Google-earth or Google-maps (in streetview!) to:
lat 43.068254 lon 1.169080

November 18th, 2014

Mormoiron and Lasserre acknowledge Grothendieck

In the series of post on Grothendieck-places I wrote a year ago (see here and links at the end) I tried to convince these French villages to update their Wikipedia page to acknowledge the existence of Grothendieck under the heading ‘Personnalités liées à la commune’, without much success.

Today it is nice to see that Lasserre added Grothendieck to their page:

“Alexandre Grothendieck (1928-2014), considéré comme un des plus grands mathématiciens du xxe siècle, y a vécu en quasi-ermite de 1990 à sa mort.”

Also Mormoiron, where Grothendieck lived in the 80ties (see picture below) has updated its page:

“Alexandre Grothendieck a habité temporairement à Mormoiron (“Les Aumettes”)”

French villages who still have to follow suit:
– Vendargues
– Massy
– Olmet-et-Villecun

November 19th, 2014

Please keep an eye on the GrothendieckCircle for updates

+Leila Schneps invested a lot of time over the years setting up the Grothendieck Circle website.

Some material had to be removed a few years ago as per Groth’s request.

I’m sure many of you will be as thrilled as I was to get this message from Leila:

“I have already started modifying the Grothendieck circle website and it will of course eventually return completely. Plus many things will be added, as we will now have access to Grothendieck’s correspondence and many other papers.”

Leila already began to update the site, for example there’s this new page on Groth’s life in Lasserre.

I understand Leila is traveling to Lasserre tomorrow, presumably for Grothendieck’s funeral. Hopefully she will eventually post something about it on the GrothendieckCircle (or, why not here on G+).

December 4th, 2014

Nicolas Bourbaki is temporarily resurrected to announce the death of Grothendieck in the French newspaper Le Monde.

You may recall that Bourbaki passed away on november 11th 1968, see +Peter Luschny’s post on his death announcement.

December 6th, 2014

The ‘avis de décès’ released by Grothendieck’s family and friends, published in the local French newspaper ‘La Depeche’, on saturday november 15th.

It announces Grothendieck’s cremation, on november 17th at 11.30h in the village of Pamiers, bordering the ‘Camp du Vernet’, where Grothendieck’s father Sasha was imprisoned, before being deported to Auschwitz and murdered by the Nazis in 1942.

June 12th, 2015

Grothendieck’s later writings

Next week there’s a Grothendieck conference at Montpellier. George Maltsiniotis will give a talk thursday afternoon with the exciting title “Grothendieck’s manuscripts in Lasserre” (hat tip +Pieter Belmans ).

You may recall that G’s last hideout was in the Pyrenean village of Lasserre.

After a bit of sleuthing around I’ve heard some great news.

Grothendieck’s family have donated all of his later writings (apart from his correspondences and other family-related stuff) to the Bibliotheque Nationale. The BNF have expressed their intention of scanning all this material (thousands of pages it seems) and making them (eventually) available online!

Rumour has it that the donation consists of 41 large folders containing G’s reflections, kept in the form of a diary (a bit like ‘Clef des Songes’), on G’s usual suspects (evil, Satan, the cosmos), but 2 or 3 of these folders contain mathematics (of sorts).

Probably, Maltsiniotis will give a preview on this material. To anyone lucky enough to be able to go down south next week and to attend his talk, please keep me in the loop…

June 19th, 2015

Maltsiniotis’ talk on Grothendieck’s Lasserre-gribouillis

Yesterday, George Maltsiniotis gave a talk at the Gothendieck conference in Montpellier with title “Grothendieck’s manuscripts in Lasserre”.

This morning, +David Roberts asked for more information on its content, and earlier i gave a short reply on what i learned, but perhaps this matter deserves a more careful write-up.

+Damien Calaque attended George’s talk and all info below is based on his recollections. Damien stresses that he didn’t take notes so there might be minor errors in the titles and order of the parts mentioned below.

EDIT: based on info i got from +Pieter Belmans in the comments below (followed up by the picture he got via +Adeel Khan taken by Edouard Balzin) i’ve corrected the order and added additional info.

The talk was videotaped and should become public soon.

As i mentioned last week Grothendieck’s family has handed over all non-family related material to the Bibliotheque Nationale. Two days ago, Le Monde wrote that the legacy consists of some 50.000 pages.

Maltsiniotis insisted that the BNF wants to make these notes available to the academic community, after they made an inventory (which may take some time).

I guess from the blackboard-picture i got from Pieter, the person responsible at the BNF is Isabelle le Masme de Chermont.

The Lasserre-griboillis themselves consists of 5 parts:

1. Géométrie élémentaire schématique. (August 1992)
This is about quadratic forms and seems to be really elementary.

2. Structure de la psyché. (12/10/1992-28/09/1993) 3600 pages
This one is about some combinatorics of oriented graphs with extra-structure (part of the structure are successor and predecessor operators on the set of arrows).

3. Psyché et structures (26/03/93-20/06/93) 700 pages
This one is non-mathematical.

4. Maxwell equations.
Maltsiniotis mentioned that he was surprised to see that there was at best one mathematics book in G’s home, but plenty of physics books.

5. Le problème du mal. (1993-1998)
This one is huge (30.000 pages) and is non-mathematical.

Note that also the Mormoiron-gribouillis will be made public by the University of Montpellier, or if you prefer video.

Finally, is the photo below what you think it is? Yep!

January 20th, 2016

where are the videos of the Grothendieck conference?

Mid june 2015 a conference “Mathematics of the 21st century: the vision of Alexander Grothendieck” was held in Montpellier. In a comment to a post here on Maltsiniotis’ talk i mentioned that most of the talks were video-taped and that they would soon be made public.

When they failed to surface on the Montpellier website, i asked +Damien Calaque for more information. Some months ago Damien told me the strange (and worrying) tale of their fate.

At that moment Damien was in a process of trying to recover the videos. Two weeks ago he told me things were looking good, so i now feel free to post about it.

Michael Wright is the head of the Archive for Mathematical Sciences & Philosophy. He arranged with the organizers of the conference that he would send someone over to video-tape the lectures and that he would make them available on his Archive. He also promised to send a copy of the videos to Montpellier, but he never did. Nor did the tapes appear on his site.

Damien Calague emailed Wright asking for more information and eventually got a reply. It appears that Wright will not be able to edit the videos nor put them online in a reasonable time.

They agreed that Damien would send him a large capacity USB-drive. Wright would copy the videos on it and send it back. Damien will arrange for the videos to be edited and the University of Montpellier will put them online. Hopefully everything will work out smoothly.

So please keep an eye on the website of l’Institut Montpelliérain Alexander Grothendieck

May 6th, 2017

Grothendieck’s Montpellier notes will hit the net May 10th

At last there is an agreement between the university at Montpellier and Grothendieck’s children to release the ‘Montpellier gribouillis’ (about 28000 pages will hit the net soon).
Another 65000 pages, found at Lasserre after Grothendieck’s death, might one day end up at the IHES or the Bibliotheque Nationale.
If you are interested in the history of Grothendieck’s notes, there is this old post on my blog.

(h/t Theo Raedschelders for the Liberation link)

May 11th, 2017

Buy a Grothendieck painting to get the Lasserre notes online!

As of yesterday, most of Grothendieck’s Montpellier notes are freely available at this site.

There’s much to say about the presentation (eg. It is not possible to link directly to a given page/article, it is scanned at only 400 dpi etc. etc.) but hey, here they are at last, for everyone to study.

By far the most colourful (in my first browsing of the archive) is cote No. 154, on ‘systeme de pseudo-droites’. You can download it in full (a mere 173 Mb).

As you know, the Montpellier notes are only a fraction of the material Grothendieck left behind. By far the largest (though probably not the most interesting, mathematically) are the Lasserre notes, which to the best of my knowledge are in the care of a Parisian bookseller.

Here’s an idea:
almost every page of No. 154 (written on ancient computer-output) looks like a painting. No doubt, most math departments in the world would love to acquire one framed page of it. Perhaps this can raise enough money to safeguard the Lasserre notes…

July 13th, 2017

le Tour de France in Grothendieck’s backyard

If you want to see the scenery Grothendieck enjoyed in his later years, watch the Tour de France tomorrow.

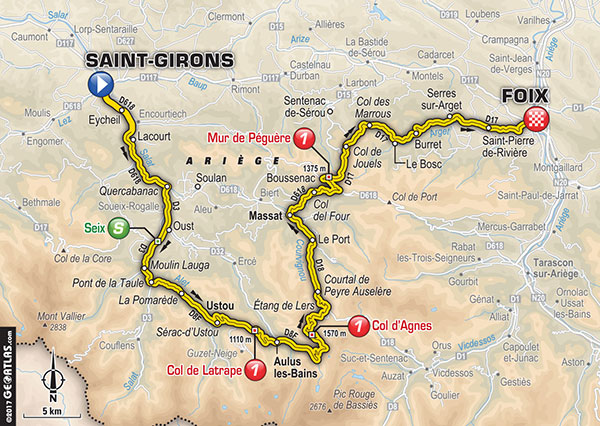
It starts in Saint-Girons where he went to the weekly market (and died in hospital, november 13th 2014), ending in Foix with 3 category 1 climbs along the way (familiar to anyone familiar with Julia Stagg’s expat-lit set at ‘Fogas’ or you can read my own post on Fogas).

It will not pass through Lasserre (where G spend the final 20 years of his life) which is just to the north of Saint-Girons.