Skip to content →

Category: web

yet another math2.0 proposal

Published February 11, 2009 by lievenlb

At present, some interesting experiments are going on exploring the potential of web 2.0 for mathematical research, that is, setting up a usable math 2.0 – environment.

The starting point is that math 2.0 should be something like blogs+extras. Most mathematicians are not that interested in the latest ICT-tools, but at least they are slowly getting used to reading blogs, so we should stick to this medium and try to enhance it for online-research.

Michael Nielsen has written a couple of posts on this : an after-dinner talk about doing science online aiming at a mathematics audience, building on an essay on the future of science.

Both posts were influential to Tim Gowers‘ dream of massively collaborative mathematics. He took an interesting problem, laid down a set of 12 rules-of-conduct and invited everyone to contribute. The project is still gaining momentum and Terry Tao is also posting about it on his blog.

Michael Nielsen compared Gowers’ approach to long established practice in the open-source software community.

Another interesting experiment is nLab, a knowledge-wiki set up by the reader-community of the n-category cafe. They describe it as : “In other words: this place is like the library, or alchemist’s laboratory, in the back room of the n-Category Café. You come here to work and go there to chat.
We are hoping to create here a space for presentation and archival storage of collaborative work of encyclopedic, didactic, expositional, but also original nature. This will include, but not be limited to, the subjects being discussed every day in the n-Café.”

Both experiments are working great, aided by the authority-status of the blogger, resp. the popularity of the blog, within the research topic. But, what about topics failing to have a blogger or blog of similar status? Should we all drop our current research-interest and convert to either combinatorics or higher-categories?

History taught us in case of failing authority we’d better settle for ‘manageable anarchy’. So, here’s my math2.0-anarchy-allowed-proposal :

  • per research-topic (say, an arXiv-topic) we’ll set up a seperate online-reasearch-environment
  • anyone interested in that topic is allowed to register and fill-out a profile linking to her list of publications, describe his research interests, her ongoing projects and other trivia
  • some may want to start a blog within the environment or join an already existing one, and should be allowed to do so
  • some may opt just to read blog posts and occasionally comment, and again, should be allowed to do so
  • some may want to set up a research-group to solve a specific problem. they may choose to do this in the open, or as a covert-operation, taking on new members only by invitation
  • some may use the environment mainly for networking or chatting-up with their friends
  • some research-groups may want to start a group-blog or knowledge-wiki to archive their finds
  • surely we’ll be not discussing math in ASCII but in latex
  • anyone will be able to follow specific sub-projects via RSS-feeds
  • anyone can see site-wide activity online, see who’s currently there and chat if they feel the need
  • anyone can do whatever sensible web2.0-thing there is I forgot by age and hence by ignorance

If this seems like a tall order to satisfy, a bit of research will show that we live at the fortunate moment in time when all the basic ingredient are there, freely available, to do just that!

Over the last weeks I’ve wasted too many hours googling for help, reading-up different fora to get it all working, but … somehow succeeded. Here’s a screen-shot of my very-own NSN (for : noncommutative-social-network) :



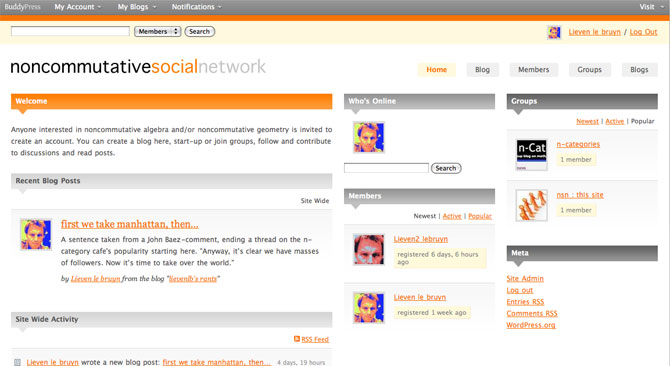
Please allow me a few more days to tidy things up and then I’ll make the link available so that anyone interested can experiment with it.

But then, I’ve no desire to spend my days web-mastering such a site. Perhaps some of you would like to take this on, provided you’d get it on a silver plate? (that is, without having to spend too much time setting it up).

So. I’ll run a series of posts explaining how to “set-up your own math2.0 environment”. I’m not aiming at the internet-savvy ones (they’ll probably do it a lot more efficiently), but at people like myself, who are interested to investigate web-based possibilities, but need to be told where to find the very basics, such as the location of their httpd.conf file or their php.ini and such.

I’ve zeroed my MacBookPro, re-installed OSX 10.5 from scratch, upgraded it to current 10.5.6 but no extras (say, vanilla 10.5.6). And I’ll guide you from there, in all gory details, with plenty of screen-shots as I would have liked to find them when I tried to set this up.

One Comment

best of 2008 (2) : big theorems

Published January 3, 2009 by lievenlb

Charles Siegel of Rigorous Trivialities ran a great series on big theorems.

The series started january 10th 2008 with a post on Bezout’s theorem, followed by posts on Chow’s lemma, Serre duality, Riemann-Roch, Bertini, Nakayama’s lemma, Groebner bases, Hurwitz to end just before christmas with a post on Kontsevich’s formula.

Also at other blogs, 2008 was the year of series of long posts containing substantial pure mathematics.

Out of many, just two examples : Chris Schommer-Pries ran a three part series on TQFTs via planar algebras starting here, at the secret blogging seminar.
And, Peter Woit of Not Even Wrong has an ungoing series of posts called Notes on BRST, starting here. At the moment he is at episode nine.

It suffices to have a quick look at the length of any of these posts, to see that a great deal of work was put into these series (and numerous similar ones, elsewhere). Is this amount of time well spend? Or, should we focus on shorter, easier digestible math-posts?

What got me thinking was this merciless comment Charles got after a great series of posts leading up to Kontsevich’s formula :

“Perhaps you should make a New Years commitment to not be so obscurantist, like John Armstrong, and instead promote the public understanding of math!”

Well, if this doesn’t put you off blogging for a while, what will?

So, are we really writing the wrong sort of posts? Do math-blog readers only want short, flashy, easy reading posts these days? Or, is anyone out there taking notice of the hard work it takes to write such a technical post, let alone a series of them?

At first I was rather pessimistic about the probable answer to all these questions, but, fortunately we have Google Analytics to quantify things a bit.

Clearly I can only rely on the statistics for my own site, so I’ll treat the case of a recent post here : Mumford’s treasure map which tried to explain the notion of a generic point and how one might depict an affine scheme.

Here’s some of the Google Analytics data :



The yellow function gives the number of pageviews for that post, the value ranges between 0 and 600 (the number to the right of the picture). In total this post was viewed 2470 times, up till now.

The blue function tells the average time a visitor spend reading that post, the numbers range between 0 and 8 minutes (the times to the left of the picture). On average the time-on-page was 2.24 minutes, so in all people spend well over 92 hours reading this one post! This seems like a good return for the time it took me to write it…

Some other things can be learned from this data. Whereas the number of page-views has two peaks early on (one the day it was posted, the second one when Peter Woit linked to it) and is now steadily decreasing, the time-on-page for the later visitors is substantially longer than the early readers.

Some of this may be explained (see comment below) by returning visits. Here is a more detailed picture (orange = new visits, green=returning visits, blue=’total’ whatever this means).



All in all good news : there is indeed a market for longer technical math-posts and people (eventually) take time to read the post in detail.

6 Comments

best of 2008 (1) : wiskundemeisjes

Published January 2, 2009 by lievenlb

Of course, excellent math-blogs exist in every language imaginable, but my linguistic limitations restrict me to the ones written in English, French, German and … Dutch. Here a few links to Dutch (or rather, Flemish) math-blogs, in order of proximity :
Stijn Symens blog, Rudy Penne’s wiskunde is sexy (math is sexy), Koen Vervloesem’s QED.

My favorite one is wiskundemeisjes (‘math-chicks’ or ‘math-girls’), written by Ionica Smeets and Jeanine Daems, two reasearchers at Leiden University. Every month they have a post called “the favorite (living) mathematician of …” in which they ask someone to nominate and introduce his/her favorite colleague mathematician. Here some examples : Roger Penrose chooses Michael Atiyah, Robbert Dijkgraaf chooses Maxim Kontsevich, Frans Oort chooses David Mumford, Gunther Cornelissen chooses Yuri I. Manin, Hendrik Lenstra chooses Bjorn Poonen, etc. the full list is here or here. This series deserves a wider audience. Perhaps Ionica and Jeanine might consider translating some of these posts?

I’m certain their English is far better than mine, so here’s a feeble attempt to translate the one post in their series they consider a complete failure (it isn’t even listed in the category). Two reasons for me to do so : it features Matilde Marcolli (one of my own favorite living mathematicians) and Matilde expresses here very clearly my own take on popular-math books/blogs.

The original post was written by Ionica and was called Weg met de ‘favoriete wiskundige van…’ :

“This week I did spend much of my time at the Fifth European Mathematical Congress in Amsterdam. Several mathematicians suggested I should have a chat with Matilde Marcolli, one of the plenary speakers. It seemed like a nice idea to ask her about her favorite (still living) mathematician, for our series.

Marcolli explained why she couldn’t answer this question : she has favorite mathematical ideas, but it doesn’t interest her one bit who discovered or proved them. And, there are mathematicians she likes, but that’s because she finds them interesting as human beings, independent of their mathematical achievements.

In addition, she thinks it’s a mistake to focus science too much on the persons. Scientific ideas should play the main role, not the scientists themselves. To her it is important to remember that many results are the combined effort of several people, that science doesn’t evolve around personalities and that scientific ideas are accessible to anyone.

Marcolli also dislikes the current trend in popular science writing: “I am completely unable to read popular-scientific books. As soon as they start telling anecdotes and stories, I throw away the book. I don’t care about their lives, I care about the real stuff.”

She’d love to read a popular science-book containing only ideas. She regrets that most of these books restrict to story-telling, but fail to disseminate the scientific ideas.”

Ionica then goes on to defend her own approach to science-popularization :

“… Probably, people will not know much about Galois-theory by reading about his turbulent life. Still, I can imagine people to become interested in ‘the real stuff’ after reading his biography, and, in this manner they will read some mathematics they wouldn’t have known to exist otherwise. But, Marcolli got me thinking, for it is true that almost all popular science-books focus on anecdotes rather than science itself. Is this wrong? For instance, do you want to see more mathematics here? I’m curious to hear your opinion on this.”

Even though my own approach is somewhat different, Ionica and Jeanine you’re doing an excellent job: “houden zo!”

One Comment