 COL is a map-coloring game invented by Colin Vout.
COL is a map-coloring game invented by Colin Vout.
Two players Left (bLack) and Right (white) take turns in coloring the
map subject to the rule that no two neighboring regions may be colored
the same. The last player to be able to move wins the game. For my talk
on combinatorial game theory in two weeks, I choose for a simplified
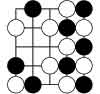
version of COL, namely COLgo which is played with go-stoned on a
(partial) go-board. Each spot has 4 neighbors (North, East, South and
West). For example, the picture on the left is a legal COLgo-position on
a 5×5 board. COL is a simple game to illustrate some of the key features
of game theory. In sharp contrast to other games, one has a general
result on the possible values of a COL-position : each position has
value $z$ or $z+\\bigstar$ where $z$ is a (Conway)-number (that is, a
dyadic integer) and where $\\bigstar$ is the fuzzy game {0|0}. In
the talk I will give a proof of this result (there are not so many
results in combinatorial game theory one can prove from scratch in 50
minutes but this is one of them). Of course, to illustrate the result I
had to find positions which have counter-intuitive values such as 1/2.
The picture on the left is an example of such a position on a 5×5 board
but surely one must be able to find 1/2-positions on a 4×4 board
(perhaps even on a 3×3?). If you have an example, please tell me.
On a slightly different matter : I used the psgo.sty package in LaTeX to print the (partial)
go-boards and positions. If I ever write out the notes I’ll post them
here but they will be in Dutch.
