 Last time we did recall Cantor’s addition and multiplication on ordinal numbers. Note that we can identify an ordinal number $\alpha $ with (the order type of) the set of all strictly smaller ordinals, that is, $\alpha = { \alpha’~:~\alpha’ < \alpha } $. Given two ordinals $\alpha $ and $\beta $ we will denote their Cantor-sums and products as $[ \alpha + \beta] $ and $[\alpha . \beta] $.
Last time we did recall Cantor’s addition and multiplication on ordinal numbers. Note that we can identify an ordinal number $\alpha $ with (the order type of) the set of all strictly smaller ordinals, that is, $\alpha = { \alpha’~:~\alpha’ < \alpha } $. Given two ordinals $\alpha $ and $\beta $ we will denote their Cantor-sums and products as $[ \alpha + \beta] $ and $[\alpha . \beta] $.
The reason for these square brackets is that John Conway constructed a well behaved nim-addition and nim-multiplication on all ordinals $\mathbf{On}_2 $ by imposing the ‘simplest’ rules which make $\mathbf{On}_2 $ into a field. By this we mean that, in order to define the addition $\alpha + \beta $ we must have constructed before all sums $\alpha’ + \beta $ and $\alpha + \beta’ $ with $\alpha’ < \alpha $ and $\beta’ < \beta $. If + is going to be a well-defined addition on $\mathbf{On}_2 $ clearly $\alpha + \beta $ cannot be equal to one of these previously constructed sums and the ‘simplicity rule’ asserts that we should take $\alpha+\beta $ the least ordinal different from all these sums $\alpha’+\beta $ and $\alpha+\beta’ $. In symbols, we define
$\alpha+ \beta = \mathbf{mex} { \alpha’+\beta,\alpha+ \beta’~|~\alpha’ < \alpha, \beta’ < \beta } $
where $\mathbf{mex} $ stands for ‘minimal excluded value’. If you’d ever played the game of Nim you will recognize this as the Nim-addition, at least when $\alpha $ and $\beta $ are finite ordinals (that is, natural numbers) (to nim-add two numbers n and m write them out in binary digits and add without carrying). Alternatively, the nim-sum n+m can be found applying the following two rules :
- the nim-sum of a number of distinct 2-powers is their ordinary sum (e.g. $8+4+1=13 $, and,
- the nim-sum of two equal numbers is 0.
So, all we have to do is to write numbers n and m as sums of two powers, scratch equal terms and add normally. For example, $13+7=(8+4+1)+(4+2+1)=8+2=10 $ (of course this is just digital sum without carry in disguise).
 Here’s the beginning of the nim-addition table on ordinals. For example, to define $13+7 $ we have to look at all values in the first 7 entries of the row of 13 (that is, ${ 13,12,15,14,9,8,11 } $) and the first 13 entries in the column of 7 (that is, ${ 7,6,5,4,3,2,1,0,15,14,13,12,11 } $) and find the first number not included in these two sets (which is indeed $10 $).
Here’s the beginning of the nim-addition table on ordinals. For example, to define $13+7 $ we have to look at all values in the first 7 entries of the row of 13 (that is, ${ 13,12,15,14,9,8,11 } $) and the first 13 entries in the column of 7 (that is, ${ 7,6,5,4,3,2,1,0,15,14,13,12,11 } $) and find the first number not included in these two sets (which is indeed $10 $).
In fact, the above two rules allow us to compute the nim-sum of any two ordinals. Recall from last time that every ordinal can be written uniquely as as a finite sum of (ordinal) 2-powers :
$\alpha = [2^{\alpha_0} + 2^{\alpha_1} + \ldots + 2^{\alpha_k}] $, so to determine the nim-sum $\alpha+\beta $ we write both ordinals as sums of ordinal 2-powers, delete powers appearing twice and take the Cantor ordinal sum of the remaining sum.
 Nim-multiplication of ordinals is a bit more complicated. Here’s the definition as a minimal excluded value
Nim-multiplication of ordinals is a bit more complicated. Here’s the definition as a minimal excluded value
$\alpha.\beta = \mathbf{mex} { \alpha’.\beta + \alpha.\beta’ – \alpha’.\beta’ } $
for all $\alpha’ < \alpha, \beta’ < \beta $. The rationale behind this being that both $\alpha-\alpha’ $ and $\beta – \beta’ $ are non-zero elements, so if $\mathbf{On}_2 $ is going to be a field under nim-multiplication, their product should be non-zero (and hence strictly greater than 0), that is, $~(\alpha-\alpha’).(\beta-\beta’) > 0 $. Rewriting this we get $\alpha.\beta > \alpha’.\beta+\alpha.\beta’-\alpha’.\beta’ $ and again the ‘simplicity rule’ asserts that $\alpha.\beta $ should be the least ordinal satisfying all these inequalities, leading to the $\mathbf{mex} $-definition above. The table gives the beginning of the nim-multiplication table for ordinals. For finite ordinals n and m there is a simple 2 line procedure to compute their nim-product, similar to the addition-rules mentioned before :
- the nim-product of a number of distinct Fermat 2-powers (that is, numbers of the form $2^{2^n} $) is their ordinary product (for example, $16.4.2=128 $), and,
- the square of a Fermat 2-power is its sesquimultiple (that is, the number obtained by multiplying with $1\frac{1}{2} $ in the ordinary sense). That is, $2^2=3,4^2=6,16^2=24,… $
Using these rules, associativity and distributivity and our addition rules it is now easy to work out the nim-multiplication $n.m $ : write out n and m as sums of (multiplications by 2-powers) of Fermat 2-powers and apply the rules. Here’s an example
$5.9=(4+1).(4.2+1)=4^2.2+4.2+4+1=6.2+8+4+1=(4+2).2+13=4.2+2^2+13=8+3+13=6 $
Clearly, we’d love to have a similar procedure to calculate the nim-product $\alpha.\beta $ of arbitrary ordinals, or at least those smaller than $\omega^{\omega^{\omega}} $ (recall that Conway proved that this ordinal is isomorphic to the algebraic closure $\overline{\mathbb{F}}_2 $ of the field of two elements). From now on we restrict to such ‘small’ ordinals and we introduce the following special elements :
$\kappa_{2^n} = [2^{2^{n-1}}] $ (these are the Fermat 2-powers) and for all primes $p > 2 $ we define
$\kappa_{p^n} = [\omega^{\omega^{k-1}.p^{n-1}}] $ where $k $ is the number of primes strictly smaller than $p $ (that is, for p=3 we have k=1, for p=5, k=2 etc.).
Again by associativity and distributivity we will be able to multiply two ordinals $< \omega^{\omega^{\omega}} $ if we know how to multiply a product
$[\omega^{\alpha}.2^{n_0}].[\omega^{\beta}.2^{m_0}] $ with $\alpha,\beta < [\omega^{\omega}] $ and $n_0,m_0 \in \mathbb{N} $.
Now, $\alpha $ can be written uniquely as $[\omega^t.n_t+\omega^{t-1}.n_{t-1}+\ldots+\omega.n_2 + n_1] $ with t and all $n_i $ natural numbers. Write each $n_k $ in base $p $ where $p $ is the $k+1 $-th prime number, that is, we have for $n_0,n_1,\ldots,n_t $ an expression
$n_k=[\sum_j p^j.m(j,k)] $ with $0 \leq m(j,k) < p $
The point of all this is that any of the special elements we want to multiply can be written as a unique expression as a decreasing product
$[\omega^{\alpha}.2^{n_0}] = [ \prod_q \kappa_q^m(q) ] $
where $q $ runs over all prime powers. The crucial fact now is that for this decreasing product we have a rule similar to addition of 2-powers, that is Conway-products coincide with the Cantor-products
$[ \prod_q \kappa_q^m(q) ] = \prod_q \kappa_q^m(q) $
But then, using associativity and commutativity of the Conway-product we can ‘nearly’ describe all products $[\omega^{\alpha}.2^{n_0}].[\omega^{\beta}.2^{m_0}] $. The remaining problem being that it may happen that for some q we will end up with an exponent $m(q)+m(q’)>p $. But this can be solved if we know how to take p-powers. The rules for this are as follows
$~(\kappa_{2^n})^2 = \kappa_{2^n} + \prod_{1 \leq i < n} \kappa_{2^i} $, for 2-powers, and,
$~(\kappa_{p^n})^p = \kappa_{p^{n-1}} $ for a prime $p > 2 $ and for $n \geq 2 $, and finally
$~(\kappa_p)^p = \alpha_p $ for a prime $p > 2 $, where $\alpha_p $ is the smallest ordinal $< \kappa_p $ which cannot be written as a p-power $\beta^p $ with $\beta < \kappa_p $. Summarizing : if we will be able to find these mysterious elements $\alpha_p $ for all prime numbers p, we are able to multiply in $[\omega^{\omega^{\omega}}]=\overline{\mathbb{F}}_2 $.
Let us determine the first one. We have that $\kappa_3 = \omega $ so we are looking for the smallest natural number $n < \omega $ which cannot be written in num-multiplication as $n=m^3 $ for $m < \omega $ (that is, also $m $ a natural number). Clearly $1=1^3 $ but what about 2? Can 2 be a third root of a natural number wrt. nim-multiplication? From the tabel above we see that 2 has order 3 whence its cube root must be an element of order 9. Now, the only finite ordinals that are subfields of $\mathbf{On}_2 $ are precisely the Fermat 2-powers, so if there is a finite cube root of 2, it must be contained in one of the finite fields $[2^{2^n}] $ (of which the mutiplicative group has order $2^{2^n}-1 $ and one easily shows that 9 cannot be a divisor of any of the numbers $2^{2^n}-1 $, that is, 2 doesn’t have a finte 3-th root in nim! Phrased differently, we found our first mystery number $\alpha_3 = 2 $. That is, we have the marvelous identity in nim-arithmetic
$\omega^3 = 2 $
Okay, so what is $\alpha_5 $? Well, we have $\kappa_5 = [\omega^{\omega}] $ and we have to look for the smallest ordinal which cannot be written as a 5-th root. By inspection of the finite nim-table we see that 1,2 and 3 have 5-th roots in $\omega $ but 4 does not! The reason being that 4 has order 15 (check in the finite field [16]) and 25 cannot divide any number of the form $2^{2^n}-1 $. That is, $\alpha_5=4 $ giving another crazy nim-identity
$~(\omega^{\omega})^5 = 4 $
And, surprises continue to pop up… Conway showed that $\alpha_7 = \omega+1 $ giving the nim-identity $~(\omega^{\omega^2})^7 = \omega+1 $. The proof of this already uses some clever finite field arguments. Because 7 doesn’t divide any number $2^{2^n}-1 $, none of the finite subfields $[2^{2^n}] $ contains a 7-th root of unity, so the 7-power map is injective whence surjective, so all finite ordinal have finite 7-th roots! That is, $\alpha_7 \geq \omega $. Because $\omega $ lies in a cubic extension of the finite field [4], the field generated by $\omega $ has 64 elements and so its multiplicative group is cyclic of order 63 and as $\omega $ has order 9, it must be a 7-th power in this field. But, as the only 7th powers in that field are precisely the powers of $\omega $ and by inspection $\omega+1 $ is not a 7-th power in that field (and hence also not in any field extension obtained by adjoining square, cube and fifth roots) so $\alpha_7=\omega +1 $.
Conway did stop at $\alpha_7 $ but I’ve always been intrigued by that one line in ONAG p.61 : “Hendrik Lenstra has computed $\alpha_p $ for $p \leq 43 $”. Next time we will see how Lenstra managed to do this and we will use sage to extend his list a bit further, including the first open case : $\alpha_{47}= \omega^{\omega^7}+1 $.
For an enjoyable video on all of this, see Conway’s MSRI lecture on Infinite Games. The nim-arithmetic part is towards the end of the lecture but watching the whole video is a genuine treat!



 Here’s the beginning of the nim-addition table on ordinals. For example, to define $13+7 $ we have to look at all values in the first 7 entries of the row of 13 (that is, ${ 13,12,15,14,9,8,11 } $) and the first 13 entries in the column of 7 (that is, ${ 7,6,5,4,3,2,1,0,15,14,13,12,11 } $) and find the first number not included in these two sets (which is indeed $10 $).
Here’s the beginning of the nim-addition table on ordinals. For example, to define $13+7 $ we have to look at all values in the first 7 entries of the row of 13 (that is, ${ 13,12,15,14,9,8,11 } $) and the first 13 entries in the column of 7 (that is, ${ 7,6,5,4,3,2,1,0,15,14,13,12,11 } $) and find the first number not included in these two sets (which is indeed $10 $). Nim-multiplication of ordinals is a bit more complicated. Here’s the definition as a minimal excluded value
Nim-multiplication of ordinals is a bit more complicated. Here’s the definition as a minimal excluded value
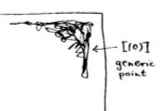 The doodle in the right upper corner depicts the
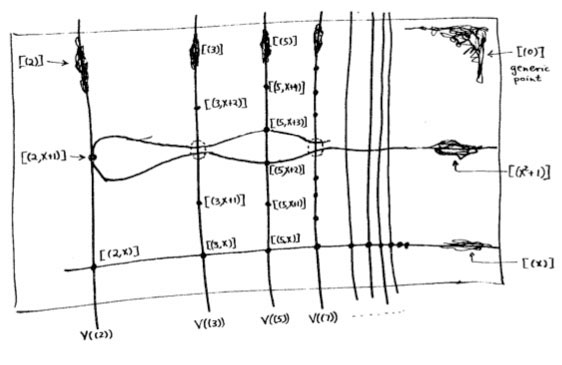
The doodle in the right upper corner depicts the 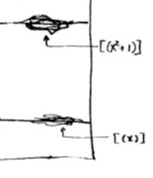 Let’s move over to the doodles in the lower right-hand corner. They represent the geometric object corresponding to principal prime ideals of the form $~(p(x)) $, where $p(x) $ in an
Let’s move over to the doodles in the lower right-hand corner. They represent the geometric object corresponding to principal prime ideals of the form $~(p(x)) $, where $p(x) $ in an  Apart from these ‘horizontal’ curves, there are also ‘vertical’ lines corresponding to the principal prime ideals $~(p) $, containing the polynomials, all of which coefficients are divisible by the prime number $p $. These are indeed prime ideals of $\mathbb{Z}[x] $, because their quotients are
Apart from these ‘horizontal’ curves, there are also ‘vertical’ lines corresponding to the principal prime ideals $~(p) $, containing the polynomials, all of which coefficients are divisible by the prime number $p $. These are indeed prime ideals of $\mathbb{Z}[x] $, because their quotients are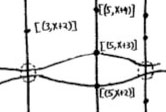 Right! So far we managed to depict the zero prime ideal (the whole plane) and the principal prime ideals of $\mathbb{Z}[x] $ (the horizontal curves and the vertical lines). Remains to depict the
Right! So far we managed to depict the zero prime ideal (the whole plane) and the principal prime ideals of $\mathbb{Z}[x] $ (the horizontal curves and the vertical lines). Remains to depict the