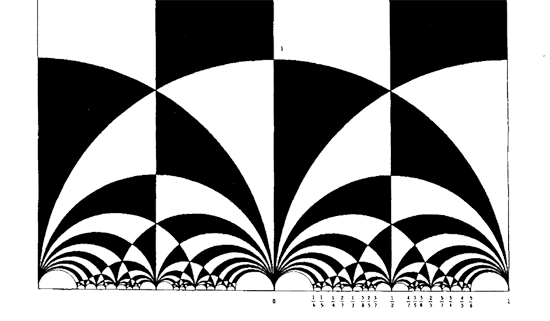
Today we will link modular quilts (via their associated cuboid tree diagrams) to special hyperbolic polygons. The above drawing gives the hyperbolic polygon (the gray boundary) associated to the M(24) tree diagram (the black interior graph). In general, the correspondence goes as follows.
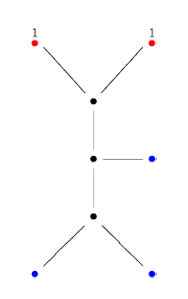
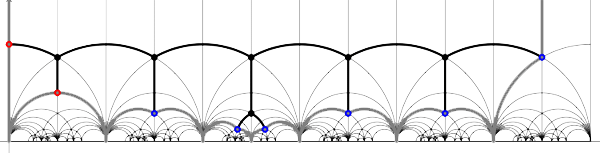
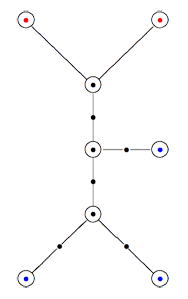 Recall that a cuboid tree diagram is a tree such that all internal vertices are 3-valent and have a specified ordering on the incident edges (given by walking counterclockwise around the vertex) and such that all leaf-vertices are tinted blue or red, the latter ones are paired via an involution (indicated by giving paired red vertices the same label). Introduce a new 2-valent vertex on all edges joining two internal vertices or a blue vertex to an internal vertex. So, the picture on the right corresponds to the tree diagram on the left. Equip this extended tree with a metric such that every edge has length equal to an f-edge in the Dedekind tessellation. Fix an edge having a red vertex and develop this isometrically onto the f-edge connecting $i $ to $\rho $ in the tessellation. Then, the extended tree develops uniquely along the f-edges of the tessellation and such that the circled black and blue vertices correspond to odd vertices, the circled red and added uncircled vertices correspond to even vertices in the tessellation. Starting from the above tree (and choosing the upper-left edge to start the embedding), we obtain the picture on the left (we have removed the added 2-valent vertices)
Recall that a cuboid tree diagram is a tree such that all internal vertices are 3-valent and have a specified ordering on the incident edges (given by walking counterclockwise around the vertex) and such that all leaf-vertices are tinted blue or red, the latter ones are paired via an involution (indicated by giving paired red vertices the same label). Introduce a new 2-valent vertex on all edges joining two internal vertices or a blue vertex to an internal vertex. So, the picture on the right corresponds to the tree diagram on the left. Equip this extended tree with a metric such that every edge has length equal to an f-edge in the Dedekind tessellation. Fix an edge having a red vertex and develop this isometrically onto the f-edge connecting $i $ to $\rho $ in the tessellation. Then, the extended tree develops uniquely along the f-edges of the tessellation and such that the circled black and blue vertices correspond to odd vertices, the circled red and added uncircled vertices correspond to even vertices in the tessellation. Starting from the above tree (and choosing the upper-left edge to start the embedding), we obtain the picture on the left (we have removed the added 2-valent vertices)
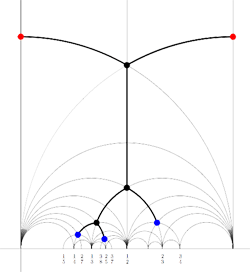
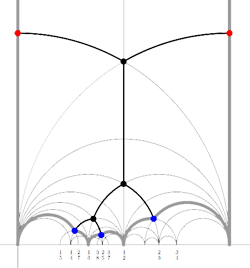
We will now associate a special hyperbolic polygon to this tree. At a red vertex take the even line going through the vertex. If under the involution the red vertex is send to itself, the even edges will be paired. Otherwise, the line is a free side and will be paired to the free side containing the red vertex corresponding under the involution. At a blue vertex, take the two odd edges making an angle of $\frac{\pi}{3} $ with the tree-edge containing the blue vertex. These odd edges will be paired. If we do this procedure for all blue and red vertices, we obtain a special polygon (see the picture on the right, the two vertical lines are paired).
Conversely, suppose we start with a special polygon such as the one on the left below
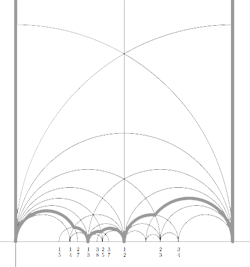
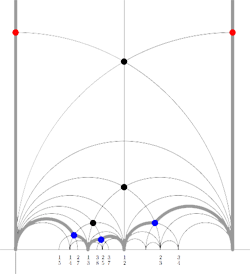
and consider all even and odd vertices on the boundary (which are tinted red, respectively blue) together with all odd vertices in the interior of the special polygon. These are indicated in the picture on the right above. If we connect these vertices with the geodesics in the polygon we get a cuboid tree diagram. This correspondence special polygons —>> tree diagrams is finite to one as we have made a choice in the starting red vertex and edge. If we would have taken the other edge containing a red vertex we would end up with the following special polygon
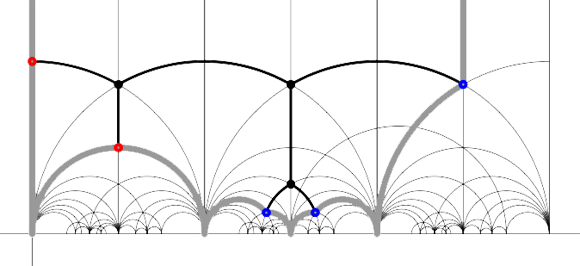
It is no accident that these two special polygons consist of exactly 24 triangles of the Dedekind tessellation as they correspond to the index 12 subgroup of the modular group $\Gamma $ determining the 12-dimensional permutation representation of the Mathieu group $M_{12} $. Similarly, the top drawing has 48 hyperbolic triangles and corresponds to the 24-dimensional permutation representation of $M_{24} $. Another time we will make the connection with Farey series which will allow us to give free generators of finite index subgroups.
Reference
Ravi S. Kulkarni, “An arithmetic-geometric method in the study of the subgroups of the modular group”, Amer. J. Math. 113 (1991) 1053-1133
One Comment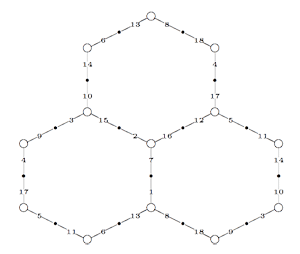 Conjugacy classes of finite index subgroups of the
Conjugacy classes of finite index subgroups of the