“Pythagorean Crimes” by Tefcros Michaelides is a murder mystery set at the beginning of the 20th century. It starts with Hilbert’s address at the 1900 ICM in Paris (in which he gives his list of problems, such as the 2nd, his program for a finitistic proof of the consistency of the axioms of arithmetic) and ends in the early 1930ties (perhaps you can by now already guess which theorem will play a crucial role in the plot?).
It depicts beautifully daily (or better, nightly) life in mathematical and artistic circles, especially in Paris between 1900 and 1906.
Bricard, Caratheodory, Dedekind, Dehn, De la Vallee-Poussin, Frege, Godel, Hadamard, Hamel, Hatzidakis, Hermite, Hilbert, Klein, Lindemann, Minkowski, Peano, Poincare, Reynaud, Russell and Whitehead all make a brief appearance, as do Appollinaire, Casagemas, Cezanne, Degas, Derain, Max Jacob, Jacobides, Lumiere, Matisse, Melies, Pallares, Picasso, Renoir, Salmon, Toulouse-Lautrec, Utrillo, Zola.

Both lists contain names I had never heard of. But the biggest surprise, to me, was to discover the name of Maurice Princet, “le mathématicien du cubisme”.
Princet (1875-1973) was a mathematician who frequented the group around Pablo Picasso at the Bateau-Lavoir in Montmartre (at least until 1907 when his wife left him for the painter Derain).
Princet introduced the group to the works of Poincare and the concept of the 4-th dimension. He gave Picasso the book “Traité élémentaire de géométrie à quatre dimensions” by Jouffret, describing hyper-cubes and other polyhedra in 4 dimensions and ways to project them dowm to the 2 dimensions of the canvas.
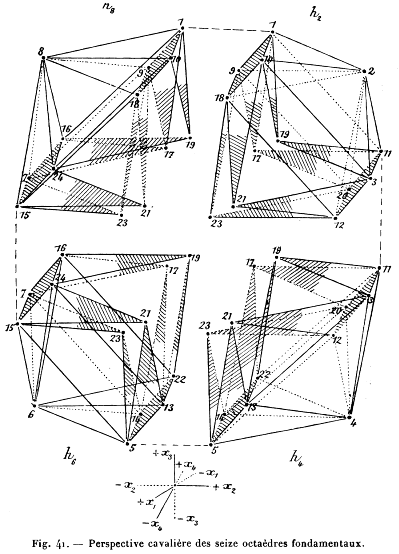
This book appears to have been influential in the genesis of Picasso’s Les Demoiselles d’Avignon (the painting also appears, in an unfinished state, in “Pythagorean Crimes”).

Some other painters tried to capture movement with projections from the 4-th dimension. A nice example is Nude descending a staircase by Marcel Duchamp (mostly known for his urinoir…).

Maurice Princet loved to get the artists interested in the new views on space. Duchamp told Pierre Cabanne, “We weren’t mathematicians at all, but we really did believe in Princet”.
I don’t know whether Duchamp liked Princet’s own attempts at painting. Here’s a cubistic work by Maurice Princet himself.