Skip to content →

Category: absolute

Quiver Grassmannians and $\mathbb{F}_1$-geometry

Published May 9, 2012 by lievenlb

Reineke’s observation that any projective variety can be realized as a quiver Grassmannian is bad news: we will have to look at special representations and/or dimension vectors if we want the Grassmannian to have desirable properties. Some people still see a silver lining: it can be used to define a larger class of geometric objects over the elusive field with one element $\mathbb{F}_1$.

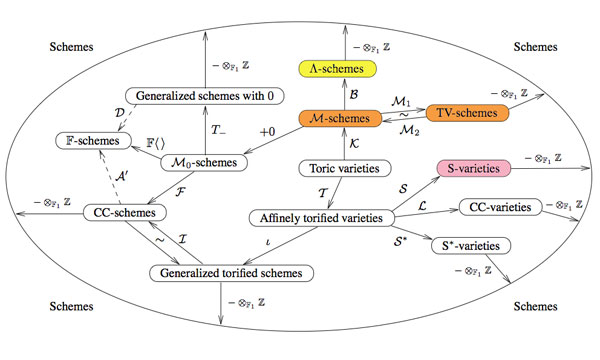
In a comment to the previous post Markus Reineke recalls motivating discussions with Javier Lopez Pena and Oliver Lorscheid (the guys responsable for the map of $\mathbb{F}_1$-land above) and asks about potential connections with $\mathbb{F}_1$-geometry. In this post I will ellaborate on Javier’s response.

The Kapranov-Smirnov $\mathbb{F}_1$-floklore tells us that an $n$-dimensional vectorspace over $\mathbb{F}_1$ is a pointed set $V^{\bullet}$ consisting of $n+1$ points, the distinguished point playing the role of the zero-vector. Linear maps $V^{\bullet} \rightarrow W^{\bullet}$ between $\mathbb{F}_1$-spaces are then just maps of pointed sets (sending the distinguished element of $V^{\bullet}$ to that of $W^{\bullet}$). As an example, the base-change group $GL_n(\mathbb{F}_1)$ of an $n$-dimensional $\mathbb{F}_1$-space $V^{\bullet}$ is isomorphic to the symmetric group $S_n$.

This allows us to make sense of quiver-representations over $\mathbb{F}_1$. To each vertex we associate a pointed set and to each arrow a map of pointed sets between the vertex-pointed sets. The dimension-vector $\alpha$ of quiver-representation is defined as before and two representations with the same dimension-vector are isomorphic is they lie in the same orbit under the action of the product of the symmetric groups determined by the components of $\alpha$. All this (and a bit more) has been worked out by Matt Szczesny in the paper Representations of quivers over $\mathbb{F}_1$.

Oliver Lorscheid developed his own approach to $\mathbb{F}_1$ based on the notion of blueprints (see also part 2 and a paper with Javier).

Roughly speaking a blueprint $B = A // \mathcal{R}$ is a commutative monoid $A$ together with an equivalence relation $\mathcal{R}$ on the monoid semiring $\mathbb{N}[A]$ compatible with addition and multiplication. Any commutative ring $R$ is a blueprint by taking $A$ the multiplicative monoid of $R$ and $\mathcal{R}(\sum_i a_i,\sum_j b_j)$ if and only if the elements $\sum_i a_i$ and $\sum_j b_j$ in $R$ are equal.

One can extend the usual notions of prime ideals, Zariski topology and structure sheaf from commutative rings to blueprints and hence define a notion of “blue schemes” which are then taken to be the schemes over $\mathbb{F}_1$.

What’s the connection with Reineke’s result? Well, for quiver-representations $V$ defined over $\mathbb{F}_1$ they can show that the corresponding quiver Grassmannians $Gr(V,\alpha)$ are blue projective varieties and hence are geometric objects defined over $\mathbb{F}_1$.

For us, old-fashioned representation theorists, a complex quiver-representation $V$ is defined over $\mathbb{F}_1$ if and only if there is an isomorphic representation $V’$ with the property that all its arrow-matrices have at most one $1$ in every column, and zeroes elsewhere.

Remember from last time that Reineke’s representation consisted of two parts : the Veronese-part encoding the $d$-uple embedding $\mathbb{P}^n \rightarrow \mathbb{P}^M$ and a linear part describing the subvariety $X \rightarrow \mathbb{P}^n$ as the intersection of the image of $\mathbb{P}^n$ in $\mathbb{P}^M$ with a finite number of hyper-planes in $\mathbb{P}^M$.

We have seen that the Veronese-part is always defined over $\mathbb{F}_1$, compatible with the fact that all approaches to $\mathbb{F}_1$-geometry allow for projective spaces and $d$-uple embeddings. The linear part does not have to be defined over $\mathbb{F}_1$ in general, but we can look at the varieties we get when we force the linear-part matrices to be of the correct form.

For example, by modifying the map $h$ of last time to $h=x_0+x_7+x_9$ we get that the quiver-representation



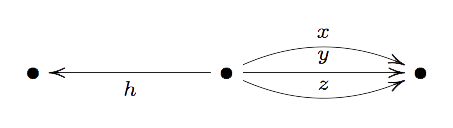
is defined over $\mathbb{F}_1$ and hence that Reineke’s associated quiver Grassmannian, which is the smooth plane elliptic curve $\mathbb{V}(x^3+y^2z+z^3)$, is a blue variety. This in sharp contrast with other approaches to $\mathbb{F}_1$-geometry which do not allow elliptic curves!

Oliver will give a talk at the 6th European Congress of Mathematics in the mini-symposium Absolute Arithmetic and $\mathbb{F}_1$-Geometry. Judging from his abstract,he will also mention quiver Grassmannians.

Leave a Comment

Manin’s three-space-2000

Published January 30, 2012 by lievenlb

Almost three decades ago, Yuri Manin submitted the paper “New dimensions in geometry” to the 25th Arbeitstagung, Bonn 1984. It is published in its proceedings, Springer Lecture Notes in Mathematics 1111, 59-101 and there’s a review of the paper available online in the Bulletin of the AMS written by Daniel Burns.

In the introduction Manin makes some highly speculative but inspiring conjectures. He considers the ring

$$\mathbb{Z}[x_1,\ldots,x_m;\xi_1,\ldots,\xi_n]$$

where $\mathbb{Z}$ are the integers, the $\xi_i$ are the “odd” variables anti-commuting among themselves and commuting with the “even” variables $x_j$. To this ring, Manin wants to associate a geometric object of dimension $1+m+n$ where $1$ refers to the “arithmetic dimension”, $m$ to the ordinary geometric dimensions $(x_1,\ldots,x_m)$ and $n$ to the new “odd dimensions” represented by the coordinates $(\xi_1,\ldots,\xi_n)$. Manin writes :

“Before the advent of ringed spaces in the fifties it would have been difficult to say precisely what me mean when we speak about this geometric object. Nowadays we simply define it as an “affine superscheme”, an object of the category of topological spaces locally ringed by a sheaf of $\mathbb{Z}_2$-graded supercommutative rings.”

Here’s my own image (based on Mumford’s depiction of $\mathsf{Spec}(\mathbb{Z}[x])$) of what Manin calls the three-space-2000, whose plain $x$-axis is supplemented by the set of primes and by the “black arrow”, corresponding to the odd dimension.

Manin speculates : “The message of the picture is intended to be the following metaphysics underlying certain recent developments in geometry: all three types of geometric dimensions are on an equal footing”.

Probably, by the addition “2000” Manin meant that by the year 2000 we would as easily switch between these three types of dimensions as we were able to draw arithmetic schemes in the mid-80ties. Quod non.

Twelve years into the new millenium we are only able to decode fragments of this. We know that symmetric algebras and exterior algebras (that is the “even” versus the “odd” dimensions) are related by Koszul duality, and that the precise relationship between the arithmetic axis and the geometric axis is the holy grail of geometry over the field with one element.

For aficionados of $\mathbb{F}_1$ there’s this gem by Manin to contemplate :

“Does there exist a group, mixing the arithmetic dimension with the (even) geometric ones?”

Way back in 1984 Manin conjectured : “There is no such group naively, but a ‘category of representations of this group’ may well exist. There may exist also certain correspondence rings (or their representations) between $\mathsf{Spec}(\mathbb{Z})$ and $x$.”

Leave a Comment

Prep-notes dump

Published December 21, 2011 by lievenlb

Here are the scans of my crude prep-notes for some of the later seminar-talks. These notes still contain mistakes, most of them were corrected during the talks. So, please, read these notes with both mercy are caution!

Hurwitz formula imples ABC : The proof of Smirnov’s argument, but modified so that one doesn’t require an $\epsilon$-term. This is known to be impossible in the number-theory case, but a possible explanation might be that not all of the Smirnov-maps $q~:~\mathsf{Spec}(\mathbb{Z}) \rightarrow \mathbb{P}^1_{\mathbb{F}_1}$ are actually covers.

Frobenius lifts and representation rings : Faithfully flat descent allows us to view torsion-free $\mathbb{Z}$-rings with a family of commuting Frobenius lifts (aka $\lambda$-rings) as algebras over the field with one element $\mathbb{F}_1$. We give several examples including the two structures on $\mathbb{Z}[x]$ and Adams operations as Frobenius lifts on representation rings $R(G)$ of finite groups. We give an example that this extra structure may separate groups having the same character table. In general this is not the case, the magic Google search term is ‘Brauer pairs’.

Big Witt vectors and Burnside rings : Because the big Witt vectors functor $W(-)$ is adjoint to the tensor-functor $- \otimes_{\mathbb{F}_1} \mathbb{Z}$ we can view the geometrical object associated to $W(A)$ as the $\mathbb{F}_1$-scheme determined by the arithmetical scheme with coordinate ring $A$. We describe the construction of $\Lambda(A)$ and describe the relation between $W(\mathbb{Z})$ and the (completion of the) Burnside ring of the infinite cyclic group.

Density theorems and the Galois-site of $\mathbb{F}_1$ : We recall standard density theorems (Frobenius, Chebotarev) in number theory and use them in combination with the Kronecker-Weber theorem to prove the result due to James Borger and Bart de Smit on the etale site of $\mathsf{Spec}(\mathbb{F}_1)$.

New geometry coming from $\mathbb{F}_1$ : This is a more speculative talk trying to determine what new features come up when we view an arithmetic scheme over $\mathbb{F}_1$. It touches on the geometric meaning of dual-coalgebras, the Habiro-structure sheaf and Habiro-topology associated to $\mathbb{P}^1_{\mathbb{Z}}$ and tries to extend these notions to more general settings. These scans are unintentionally made mysterious by the fact that the bottom part is blacked out (due to the fact they got really wet and dried horribly). In case you want more info, contact me.

Leave a Comment