Skip to content →

Author: lievenlb

la chasse

Published November 2, 2004 by lievenlb

< Monday morning 7 am : the first gunshots can be heard in the distance. As the morning progresses they come closer and one can hear the hunting dogs clearly. A bit later four or five white mini-vans race up the road and turn to get to the ridge of the mountain, each having one or more dogs inside. Fifteen minutes later, we have eyesight contact with “les chasseurs” and the gunshots are so nearby that one might consider taking cover … A typical sunday in l'Ardeche-Cevenolle (I know, it is monday but yesterday the weather was just too bad and luckily for them it's a holiday today).

The weather is really nice and as every other
addicted cyclist I want to seize the opportunity because it is highly
uncertain that there will be another dry day this week. I would like
to do my favourite round-trip : to Dompnac, then Pourcharesse and back
via St-Melany.


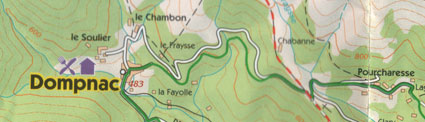
If you ever did this you will never forget the
Dompnac-Pourcharesse part of the trip : it is merely 4km but if you
know how to read a map you will understand what I mean. Unfortunately,
afterwards one has to descend to St-Melany crossing the hunting
forests of the community and I have no desire to end up in the
statistics as one of the over 70 deads or seriously wounded by
hunting-accidents in France every year …

So, I did
choose the second hardest (but safer) route : first to descend to the
bridge below and then climb to Sablieres (takes 15 min), descend to
the Drobie (4 mins) and then the serious climb to the highest road in
the vicinity at Peyre (takes 45 min) and back. The first time I did
the 'col de Peyre' I had to stop three times but now I know
one has to divide the thrip into three parts : the first part,
climbing to 'Le Mas' is fairly hard and by far the longest
part, after Le Mas one has a km which isn't that steep and one
needs to use this to recuperate a bit because the last part, when you
have the ridge of the mountain in sight, has still some very steep
streches. As this was my first cycling trip in the mountains in over
two months it was still pretty hard and I was glad to see the stone
pillar indicating the summit.

There was hardly any traffic :
7 cars and just 1 other cyclist. But I came across quite a few hunting
dogs that had lost their group. At first it is a bit scary to be on a
lonely road facing an unescorted dog but these hunting dogs are
usually rather nice. On the final climb back I met one who just turned
round and followed me whole the way back to LeTravers and stayed there
for the rest of the afternoon.

Later on, another lost dog
turned up and decided to stay as well. The local etiquette then
demands that you phone the owner(s) (the telephone numbers are written
on a collar they wear), which we did later on when we thought 'la
chasse' was ended for the day and the dogs were picked up around 8
pm. Unknowingly we did exactly the right thing to get our yearly piece
of fresh wild boar (to be continued)…

Leave a Comment

connected

Published November 1, 2004 by lievenlb

If this message gets posted it will mean that I finally
succeeded in connecting LeTravers to the rest of the world…
Clearly not via cable but using good old dial-in. I don't think
I'll ever see cable appearing here.

Electricity made it
appearance here only 10 years ago (and is an end-of-network setup
meaning that if two people on the mountain use a microwave, all lights
are dimmed…) and since 5 years one can reach us by telephone.

Since then I've been trying to get email working using
all sorts of (Belgian) dial-in adresses but nothing worked, the modem
didn't seem to be working. It turned out that in France you first
have to buy a special socket for the telephone outlet (costs 50FF)
which our neighbors promised to provide by the next time we came
along.

So, next time expectations were high and sure enough
I could hear the typical modem-noises until they got into an infinite
loop without ever making the connection.

Some people were
luckier but then they used a Windows-clone and even mimicking their
connection on a Mac didn't work. For some mysterious reason it
seemed that Macintosh computers (or at least their modems) were
incompatible with FranceTelecom.

Last week I did try
another option : I got a webpage with all free internet providers and
applied for a username-password with two of them (FreeFrance and
Tiscali). FreeFrance promised to send a package with the post whereas
Tiscali immediately replied with a dial-in nummer, username and
allowed me to set up my own password.

So, after driving
1000km (half of which in the pouring rain) and enjoying a glass of
rose outside in the setting sun (picture) I tried the Tiscali
connection without too much hope, but I think it works.

It
was a beautiful sunny afternoon (it seems it has been raining here
more or less continuously for the last three weeks) but at sunset the
clouds were rather threatening and sure enough the following day
(sunday) we spend the day within rain clouds.

Leave a Comment

double Poisson algebras

Published October 26, 2004 by lievenlb

This morning,
Michel Van den Bergh posted an interesting paper on the arXiv
entitled Double
Poisson Algebras. His main motivation was the construction of a
natural Poisson structure on quotient varieties of representations of
deformed multiplicative preprojective algebras (introduced by
Crawley-Boevey and Shaw in Multiplicative
preprojective algebras, middle convolution and the Deligne-Simpson
problem) which he achieves by extending his double Poisson structure
on the path algebra of the quiver to the 'obvious' universal
localization, that is the one by inverting all $1+aa^{\star} $ for $a $ an
arrow and $a^{\star} $ its double (the one in the other direction).
For me the more interesting fact of this paper is that his double
bracket on the path algebra of a double quiver gives finer information
than the _necklace Lie algebra_ as defined in my (old) paper with Raf
Bocklandt Necklace
Lie algebras and noncommutative symplectic geometry. I will
certainly come back to this later when I have more energy but just to
wet your appetite let me point out that Michel calls a _double bracket_
on an algebra $A $ a bilinear map
$\{ \{ -,- \} \}~:~A \times A
\rightarrow A \otimes A $
which is a derivation in the _second_
argument (for the outer bimodulke structure on $A $) and satisfies
$\{ \{ a,b \} \} = – \{ \{ b,a \} \}^o $ with $~(u \otimes v)^0 = v
\otimes u $
Given such a double bracket one can define an ordinary
bracket (using standard Hopf-algebra notation)
$\{ a,b \} = \sum
\{ \{ a,b \} \}_{(1)} \{ \{ a,b \} \}_{(2)} $
which makes $A $ into
a Loday
algebra and induces a Lie algebra structure on $A/[A,A] $. He then
goes on to define such a double bracket on the path algebra of a double
quiver in such a way that the associated Lie structure above is the
necklace Lie algebra.

2 Comments