Clearly, someone who
subscribed to your brain shouldn’t have to check the arXiv every morning only to find out
that you still haven’t posted _the_ paper s(h)e is expecting of
you, based on your recent BrainActivity…
So why not
package this into your Brain subscription? It is easy enough to get all
posts by a specific author from the archive but, unfortunately, the
arXiv doesn’t provide RSS-feeds of this information (at least, not to my
knowledge). Still, it is possible to fix this with a tiny
Perl-script.
So copy the code and adjust it replacing MyInfo
by Yours (or sligthly safer, get the arxivpost.pl
file as I had to add a few spaces to get it un-parsed) and safe it
somewhere on your system.
So how to put this to use? Btw. I know
that all of you know this by heart and that I may have given you the
(false, i swear) illusion to be fairly knowledgeable writing a
Perl-script in half an hour, but believe me, in two months (and sooner
when it’s up to me) I will have completely eradicated all this
techie-stuff from MyBrain. Then, it will take me infinitely longer to
remember/reconstruct things than it will take me now to blog this here,
so please either bear with me or go somewhere more interesting.
You’d better have Perl installed on your system, but then you have to
install extra modules from CPAN the
Comprehensive Perl Archive Network (this is to Perl what CTAN is to TeX for the mathematicians
among us). That’s pretty easy if you remember the correct commands. The
generic way to do this is by firing up your Terminal and typing things
like
iBookLieven:~ lieven$ sudo perl -MCPAN -e shell
Password: cpan shell -- CPAN exploration and modules installation
(v1.83) ReadLine support enabled cpan> install Template::Extract
and similarly for the other modules you’ll need,
LWP::Simple and XML::RSS. You may be asked questions but just go for the
default. If something goes wrong and you get a message that the module
failed to install, you have to go for a manual override…
Go to CPAN and do a search on the module’s name. You’ll
be given a list op files to download, go for the one you need and
download the souce somewhere. Then, again in Terminal do the following
routine
- cd to the downloaded and extracted directory
- perl Makefile.PL
- make
- make test
- sudo make install
Even if the test fails with
certain errors, just go ahead (it will not matter for the trivial uses
we have for these modules) and the last command is Mac OSX only (I’m
pretty certain that Linux-fanatics know what to do instead and for
Windows-diehards, well….).
Having all modules installed
you can execute the file with
perl arxivpost.pl
(assuming you created the Directory in which the program
is supposed to safe the arxivXXX.rdf file and assuming you made it
writable). That’s it. You now have your own RSS feeds of all your papers
on the arXiv which you should make for of YourBrain subscription).
Just one more thing you should do. Make this a cron
job. Check at what local time the arXiv puts online the new papers
of the day (assume it is 3am) then do a sudo crontab -e
and then add a line to the file as
5 3 * * Mon-Fri perl
/pathtowhereitis/arxivpost.pl
and your subscribers will
only have to wait 5 minutes to know whether you did it…(or not).
You can check it out either by subscribing to MyBrain or subscribing to
http://www.
neverendingbooks.org/FOAF/arxivLLB.rdf.
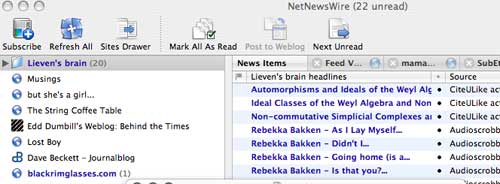 which
which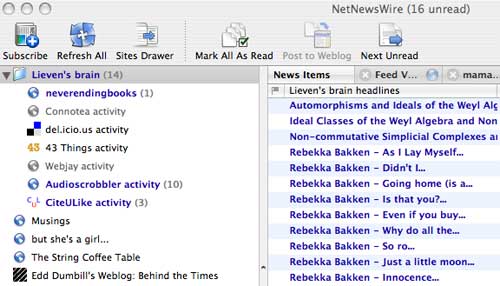 which tells
which tells appear on
appear on