COL is a map-colouring game, attibuted to Colin Vout. COLgo is COL played with Go-stones on a go-board.
The two players, bLack (left) and white (right) take turns placing a stone of their colour on the board, but two stones of the same colour may not be next to each other.
The first player unable to make a legal move looses this game.
As is common in combinatorial game theory we do not specify which player has the move. There are $4$ different outcomes, the game is called:
– positive, if there is a winning strategy for Left (bLack),
– negative, if there is a winning strategy for Right (white),
– zero, if there is a winning strategy for the second-player,
– fuzzy, if there is a winning strategy for the first player.
Here’s an endgame problem: who wins this game?

Spoiler alert: solution below.
First we can exclude all spots which are dead, that is, are excluded for both players. Example, F11 is dead because it neighbors a black as well as a white stone, but F10 is alive as it can be played by white (Right).
If we remove all dead spots, we are left with 4 regions (the four extremal corners of the board) as well as 5 spots, 3 for white and 2 for black.
That is, the game reduces to this “sum”-game, in which a player chooses one of the regions and does a legal move in that component, or takes a stone of its own colour from the second row.
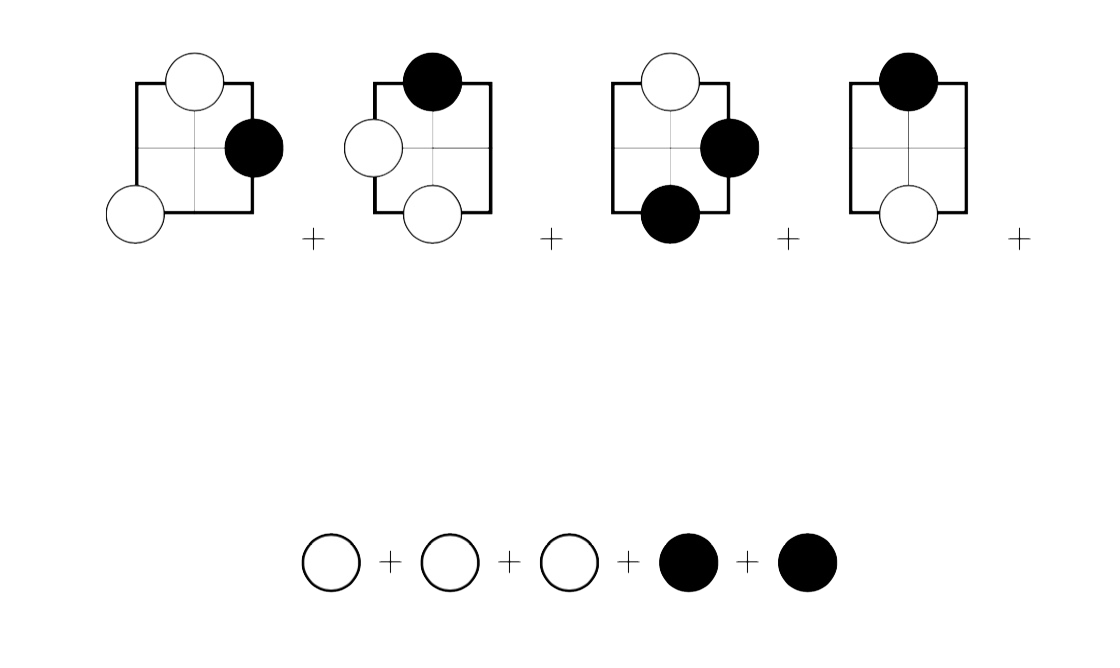
Next, we have to give a value to each of the region-games.
– the right-most game has value $0$ as the second player has a winning strategy by reflecting the first player’s move with respect to the central (dead) spot.
– the left-most game is equivalent to one black stone. Black can make two moves in the game, independent of the only move that white can make. So it has value $+1$.
– the sum-game of the two middle games has value zero. The second player can win by mirroring the first player’s move in the other component. This is called the Tweedledee-Tweedledum argument.
But then, the total value of the endgame position is
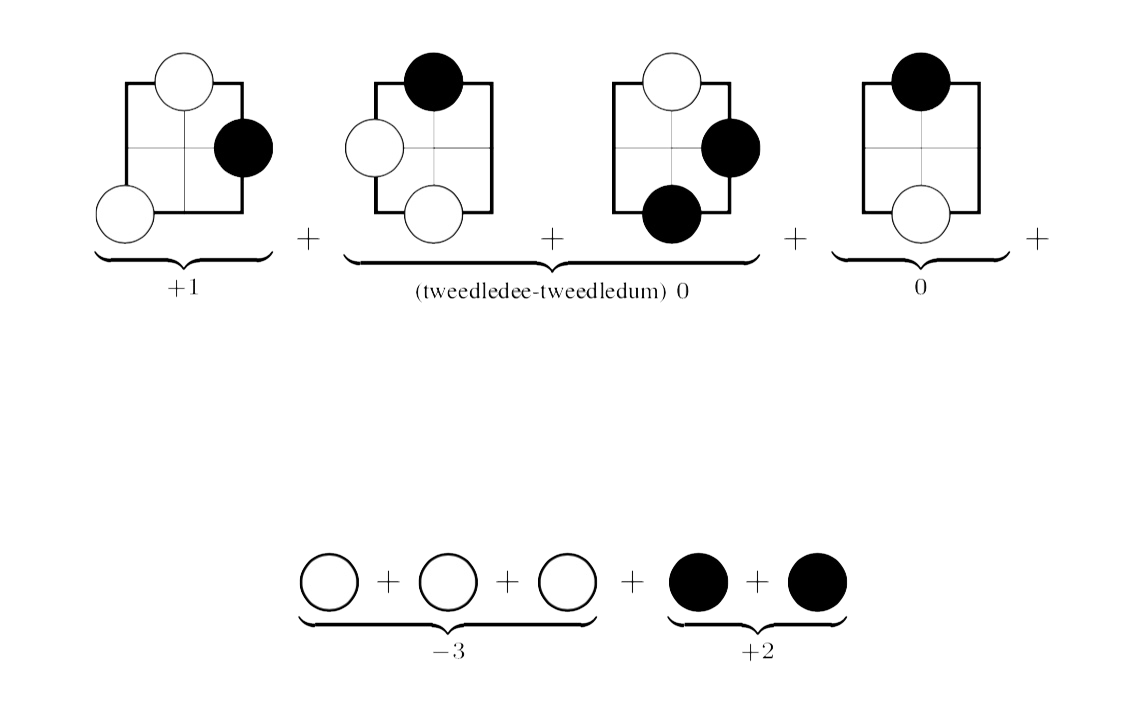
zero, so the first player to move looses the game!
Comments